Quantcast
Channel: Bharatkalyan97
Viewing all articles
Browse latest Browse all 11039
↧

Cipher writing of ancient India was called mlecchita vikalpa, pre-alphabetic, pre-syllabic cryptography of Indus Script Corpora

April 29, 2015, 9:56 pm
$
0
0
Cipher writing of ancient India was called mlecchita vikalpa, pre-alphabetic, pre-syllabic cryptography of Indus Script Corpora


The Indus writing system was NOT intended to be a secretive communication system, but could be decrypted and realized by anyone knowing the key. The key is simple: Meluhha language words which are denoted by the pictures (hieroglyphs) and similar-sounding words signifying metalwork by Meluhha artisans. 

An authorized person who could unravel the communicated message was one with the knowledge of Meluhha (mleccha) language words for the picture and for items of metalwork. 

Such persons were Bharatam Janam mentioned by Visvamitra in Rigveda. Bharatam Janam means 'metalcaster folk'. They were referred to as Meluhha in cuneiform texts.

The earliest evidence of cipher-writing in human history is recorded on a potsherd discovered (dated ca. 3300 BCE) in Harappa by HARP (Harvard Archaeology Research Project) inscribed with a hieroglyph. 

The underlying language used was Meluhha and pre-dated the invention of alphabetic or syllabic writing systems and later-day developments in encryption methods (for converting plain texts into cipher texts), cryptography and cryptology, apart from secret military messaging systems.

Five-petalled flower is tagaraka 'tabernae montana'. Rebus: tagara 'tin (metal)'. A hieroglyph signifying this flower is repeated thrice: Hieroglyph: kolmo 'three' rebus: kolami 'smithy, forge'.

The cipher is simple engineering and dramatic. What is consigned in the pot on which the inscription was inscribed was NOT tagaraka, 'fragrant flower used as a fragrance oil for the hair' but a metal which was signified by a similar sounding word: tagara in Meluhha language.

The cipher writing system of ancient India was called mlecchita vikalpa because of the following meanings associated with the two words of the phrase:

म्लेच्छित mfn. = म्लिष्ट Pa1n2. 7-2 , 18 Sch. mfn. spoken indistinctly Pan. 7-2 , 18 (Monier-Williams, p. 837, p. 838)
वि-कल्प m. alternation , alternative , option S3rS. Mn. VarBr2S. &c ( °पेन ind. " optionally "); contrivance , art Ragh. (Monier-Williams, p. 950, 955).

The phrase mlecchita vikalpa is used by Vātstyāyana in reference to cipher writing of or by mleccha.


Thus, the tin metal referred to in parole, vaak, vernacular speech as tagara was denoted by a similar sounding word tagaraka. To signify this latter word, a picture of the tagaraka flower with 5 petals was used. Thus, there was a layered rebus-metonymy constituting the cipher. Rebus was deployed by use of picture-writing, i.e. use of pictures to denote the underlying spoken word. Metonymy layer was deployed to refer to metalwork denoted by similar sounding word. A writing system was born to support trade of metalwork by seafaring merchants, across linguistic areas.

Same rebus-metonymy layer applies to another hieroglyph-- 'rim of jar':
On this Daimabad seal, the 'rim of jar' is signified.

In Meluhha language, the word was karNika 'rim of jar'. Rebus-metonymy layer yields a similar sounding word karNI 'supercargo' of a seafaring merchant. Almost all inscriptions in Indus Script Corpora are metalwork catalogs and when this hierolyph of 'rim of jar' is used in a major segment of the inscriptions, the message is that the supercargo consignments of metalwork are signified by the message which is a 'written' record of such consignments transmitted through seafaring Meluhha merchants.

When this hieroglyph appears, the intent is NOT to record a consignment of pottery of rimmed jars, but to record the message that the consignment is of metalwork supercargo. Thus, together with rebus method (similar sounding words), metonymy is used which is the substitution of the name of an attribute or adjunct for that of the thing meant. The thing meant is NOT pottery but consignment of supercargo of metalwork, karNI.

A comparable rebus-metonymy cipher using Egyptian language is shown on Narmer palette. The syllables Nar and Mer in the name are rendered rebus by the hieroglyphs of 'cuttle fish' and 'awl' to signify words N'r and M'r respectively, which syllables are read together as Narmer. A writing system comparable to Indus Script is witnessed in Egypt.
Narmer bust statue.
Palette of King Narmer, from Hierakonpolis, Egypt, Predynastic, c. 3000-2920 B.C.E., slate, 2' 1" high (Egyptian Museum, Cairo)

Such rebus-metonymy layered encryptions and decryptions in Meluhha (Mleccha) are reinforced by the following examples of inscriptions reported in the just-released Dholavira Excavation Report (2015).
117 antelope; sun motif
 40 Three-headed animal, plant; sun motif

Hieroglyph: arka 'sun' Rebus: arka 'copper' (Kannada) eraka 'moltencast copper'(Tulu) அருக்கம்¹ arukkam, n. < arka. (நாநார்த்த.) 1. Copper; செம்பு. 
(Tamil) అగసాలి (p. 0023) [ agasāli ] or అగసాలెవాడు agasāli. [Tel.] n. A goldsmith. కంసాలివాడు.(Telugu) Kannada (Kittel lexicon):

Hieroglyph: mlekh 'goat' Rebus: milakkhu 'copper' mleccha 'copper'
Hieroglyph: kolmo 'sprout' Rebus: kolami 'smithy, forge'

Hieroglyph: barad, barat 'ox' Rebus: भरत (p. 603) [ bharata ] n A factitious metal compounded of copper, pewter, tin &c.(Marathi)
Hieroglyph: one-horned young bull: खोंड (p. 216) [ khōṇḍa ] m A young bull, a bullcalf.(Marathi) खोंडरूं [ khōṇḍarūṃ ] n A contemptuous form of खोंडा in the sense of कांबळा-cowl.खोंडा [ khōṇḍā ] m A कांबळा of which one end is formed into a cowl or hood. खोंडी [ khōṇḍī ] f An outspread shovelform sack (as formed temporarily out of a कांबळा, to hold or fend off grain, chaff &c.)

Hieroglyph: kōḍ 'horn' Rebus: kōḍ 'place where artisans work, workshop' কুঁদন, কোঁদন [ kun̐dana, kōn̐dana ] n act of turning (a thing) on a lathe; act of carving (Bengali) कातारी or कांतारी (p. 154) [ kātārī or kāntārī ] m (कातणें) A turner.(Marathi)

Rebus: खोदकाम [ khōdakāma ] n Sculpture; carved work or work for the carver.
खोदगिरी [ khōdagirī ] f Sculpture, carving, engraving: also sculptured or carved work.खोदणें [ khōdaṇēṃ ] v c & i ( H) To dig. 2 To engraveखोदींव [ khōdīṃva ] p of खोदणें Dug. 2 Engraved, carved, sculptured.

Hieroglyph: horn: Ta. kōṭu (in cpds. kōṭṭu-) horn, tusk, branch of tree, cluster, bunch, coil of hair, line, diagram, bank of stream or pool; kuvaṭu branch of a tree;kōṭṭāṉ, kōṭṭuvāṉ rock horned-owl (cf. 1657 Ta. kuṭiñai). Ko. ko·ṛ (obl. ko·ṭ-) horns (one horn is kob), half of hair on each side of parting, side in game, log, section of bamboo used as fuel, line marked out. To. kwit horn, branch, path across stream in thicket. Ka.kōḍu horn, tusk, branch of a tree; kōr̤ horn. Tu. kōḍů, kōḍu horn. Te. kōḍu rivulet, branch of a river. Pa. kōḍ (pl. kōḍul) horn. Ga. (Oll.) kōr (pl.kōrgul) id. Go. (Tr.) kōr (obl. kōt-, pl. kōhk) horn of cattle or wild animals, branch of a tree; (W. Ph. A. Ch.) kōr (pl. kōhk), (S.) kōr (pl. kōhku), (Ma.)kōr̥u (pl. kōẖku) horn; (M.) kohk branch (Voc. 980); (LuS.) kogoo a horn. Kui kōju (pl. kōska) horn, antler. (DEDR 2200)
 
Hieroglyph: Te. kōḍiya, kōḍe young bull; adj. male (e.g. kōḍe dūḍa bull calf), young, youthful; kōḍekã̄ḍu a young man. Kol. (Haig) kōḍē bull. Nk. khoṛemale calf. Konḍa kōḍi cow; kōṛe young bullock. Pe. kōḍi cow. Manḍ. kūḍi id. Kui kōḍi id., ox. Kuwi (F.) kōdi cow; (S.) kajja kōḍi bull; (Su. P.) kōḍicow. (DEDR 2199)

Rebus: kũdār ‘turner’ (Bengali)

http://bharatkalyan97.blogspot.in/2015/04/excavations-at-dholavifra-1989-2005-rs.html

A string of articles on History of Cryptology and Cryptography recollected in the context of the present-day digital inscription systems and security of information substituted by digital recordings is appended to show how this early mlecchita vikalpa (cipher system of writing spoken Meluhha/Mleccha words) developed into secure encryption systems to ensure the integrity and fidelity of information transmission.

S. Kalyanaraman Sarasvati Research Center April 30, 2015

See: http://www.cs.xu.edu/math/math316/09s/00History.pdf History of Cryptology, historical timeline.

History of cryptology


Cryptology, science concerned with data communication and storage in secure and usually secret form. It encompasses both cryptography and cryptanalysis.
The term cryptology is derived from the Greek kryptós (“hidden”) and lógos (“word”). Security obtains from legitimate users being able to transform information by virtue of a secret key or keys—i.e., information known only to them. The resulting cipher, although generally inscrutable and not forgeable without the secret key, can be decrypted by anyone knowing the key either to recover the hidden information or to authenticate the source. Secrecy, though still an important function in cryptology, is often no longer the main purpose of using a transformation, and the resulting transformation may be only loosely considered a cipher.

Cryptography (from the Greek kryptós and gráphein, “to write”) was originally the study of the principles and techniques by which information could be concealed in ciphers and later revealed by legitimate users employing the secret key. It now encompasses the whole area of key-controlled transformations of information into forms that are either impossible or computationally infeasible for unauthorized persons to duplicate or undo.
Cryptanalysis (from the Greek kryptós and analýein, “to loosen” or “to untie”) is the science (and art) of recovering or forging cryptographically secured information without knowledge of the key. Cryptology is often—and mistakenly—considered a synonym for cryptography and occasionally for cryptanalysis, but specialists in the field have for years adopted the convention that cryptology is the more inclusive term, encompassing both cryptography and cryptanalysis.
Cryptography was initially only concerned with providing secrecy for written messages, especially in times of war. Its principles apply equally well, however, to securing data flowing between computers or data stored in them, to encrypting facsimile and television signals, to verifying the identity of participants in electronic commerce (e-commerce) and providing legally acceptable records of those transactions. Because of this broadened interpretation of cryptography, the field of cryptanalysis has also been enlarged.
This article discusses the basic elements of cryptology, delineating the principal systems and techniques of cryptography as well as the general types and procedures of cryptanalysis. It also provides a concise historical survey of the development of cryptosystems and cryptodevices. A brief introduction is also given to the revolution in cryptology brought on by the information age, e-commerce, and the Internet. For additional information on the encoding and encryption of facsimile and television signals and of computer data, see telecommunications system andinformation processing.

General considerations

Because much of the terminology of cryptology dates to a time when written messages were the only things being secured, the source information, even if it is an apparently incomprehensible binary stream of 1s and 0s, as in computer output, is referred to as the plaintext. As noted above, the secret information known only to the legitimate users is the key, and the transformation of the plaintext under the control of the key into a cipher (also called ciphertext) is referred to asencryption. The inverse operation, by which a legitimate receiver recovers the concealed information from the cipher using the key, is known as decryption.

The fundamentals of codes, ciphers, and authentication

The most frequently confused, and misused, terms in the lexicon of cryptology are code andcipher. Even experts occasionally employ these terms as though they were synonymous.
A code is simply an unvarying rule for replacing a piece of information (e.g., letter, word, or phrase) with another object, but not necessarily of the same sort; Morse code, which replacesalphanumeric characters with patterns of dots and dashes, is a familiar example. Probably the most widely known code in use today is the American Standard Code for Information Interchange (ASCII). Employed in all personal computers and terminals, it represents 128 characters (and operations such as backspace and carriage return) in the form of seven-bit binary numbers—i.e., as a string of seven 1s and 0s. In ASCII a lowercase a is always 1100001, an uppercase A always 1000001, and so on. Acronyms are also widely known and used codes, as, for example, Y2K (for “Year 2000”) and COD (meaning “cash on delivery”). Occasionally such a code word achieves an independent existence (and meaning) while the original equivalent phrase is forgotten or at least no longer has the precise meaning attributed to the code word—e.g.,modem (originally standing for “modulator-demodulator”).
Ciphers, as in the case of codes, also replace a piece of information (an element of the plaintext that may consist of a letter, word, or string of symbols) with another object. The difference is that the replacement is made according to a rule defined by a secret key known only to the transmitter and legitimate receiver in the expectation that an outsider, ignorant of the key, will not be able to invert the replacement to decrypt the cipher. In the past, the blurring of the distinction between codes and ciphers was relatively unimportant. In contemporary communications, however, information is frequently both encoded and encrypted so that it is important to understand the difference. A satellite communications link, for example, may encode information in ASCII characters if it is textual, or pulse-code modulate and digitize it in binary-coded decimal (BCD) form if it is an analog signal such as speech. The resulting coded data is then encrypted into ciphers by using the Data Encryption Standard or the Advanced Encryption Standard (DES or AES; described in the section History of cryptology). Finally, the resulting cipher stream itself is encoded again, using error-correcting codes for transmission from the ground station to the orbiting satellite and thence back to another ground station. These operations are then undone, in reverse order, by the intended receiver to recover the original information.
In the simplest possible example of a true cipher, A wishes to send one of two equally likely messages to B, say, to buy or sell a particular stock. The communication must take place over a wireless telephone on which eavesdroppers may listen in. It is vital to A’s and B’s interests that others not be privy to the content of their communication. In order to foil any eavesdroppers, Aand B agree in advance as to whether A will actually say what he wishes B to do, or the opposite. Because this decision on their part must be unpredictable, they decide by flipping a coin. If heads comes up, A will say Buy when he wants B to buy and Sell when he wants B to sell. If tails comes up, however, he will say Buy when he wants B to sell, and so forth. (The messages communicate only one bit of information and could therefore be 1 and 0, but the example is clearer using Buyand Sell.)
With this encryption/decryption protocol being used, an eavesdropper gains no knowledge about the actual (concealed) instruction A has sent to B as a result of listening to their telephone communication. Such a cryptosystem is defined as “perfect.” The key in this simple example is the knowledge (shared by A and B) of whether A is saying what he wishes B to do or the opposite. Encryption is the act by A of either saying what he wants done or not as determined by the key, while decryption is the interpretation by B of what A actually meant, not necessarily of what he said.
This example can be extended to illustrate the second basic function of cryptography, providing a means for B to assure himself that an instruction has actually come from A and that it is unaltered—i.e., a means of authenticating the message. In the example, if the eavesdropper intercepted A’s message to B, he could—even without knowing the prearranged key—cause B to act contrary to A’s intent by passing along to B the opposite of what A sent. Similarly, he could simply impersonate A and tell B to buy or sell without waiting for A to send a message, although he would not know in advance which action B would take as a result. In either event, the eavesdropper would be certain of deceiving B into doing something that A had not requested.
To protect against this sort of deception by outsiders, A and B could use the following encryption/decryption protocol.
They secretly flip a coin twice to choose one of four equally likely keys, labeled HH, HT, TH, and TT, with both of them knowing which key has been chosen. The outcome of the first coin flip determines the encryption rule just as in the previous example. The two coin flips together determine an authentication bit, 0 or 1, to be appended to the ciphers to form four possible messages: Buy-1, Buy-0, Sell-1, and Sell-0. B will only accept a message as authentic if it occurs in the row corresponding to the secret key. The pair of messages not in that row will be rejected byB as non-authentic. B can easily interpret the cipher in an authentic message to recover A’s instructions using the outcome of the first coin flip as the key. If a third party C impersonates Aand sends a message without waiting for A to do so, he will, with probability 1/2, choose a message that does not occur in the row corresponding to the key A and B are using. Hence, the attempted deception will be detected by B, with probability 1/2. If C waits and intercepts a message from A, no matter which message it is, he will be faced with a choice between two equally likely keys that A and B could be using. As in the previous example, the two messages he must choose between convey different instructions to B, but now one of the ciphers has a 1 and the other a 0 appended as the authentication bit, and only one of these will be accepted by B. Consequently, C’s chances of deceiving B into acting contrary to A’s instructions are still 1/2; namely, eavesdropping on A and B’s conversation has not improved C’s chances of deceiving B.
Clearly, in either example, secrecy or secrecy with authentication, the same key cannot be reused. If C learned the message by eavesdropping and observed B’s response, he could deduce the key and thereafter impersonate A with certainty of success. If, however, A and B chose as many random keys as they had messages to exchange, the security of the information would remain the same for all exchanges. When used in this manner, these examples illustrate the vital concept of a onetime key, which is the basis for the only cryptosystems that can be mathematically proved to be cryptosecure. This may seem like a “toy” example, but it illustrates the essential features of cryptography. It is worth remarking that the first example shows how even a child can create ciphers, at a cost of making as many flips of a fair coin as he has bits of information to conceal, that cannot be “broken” by even national cryptologic services with arbitrary computing power—disabusing the lay notion that the unachieved goal of cryptography is to devise a cipher that cannot be broken.

Cryptology in private and commercial life

At the very end of the 20th century, a revolution occurred in the way private citizens and businesses made use of and were dependent on pure information, i.e., information with no meaningful physical embodiment. This was sparked by two technical developments: an almost universal access to affordable real-time global communications, and the practical capability to acquire, process, store, and disseminate virtually unlimited amounts of information. Electronic banking, personal computers, the Internet and associated e-commerce, and “smart” cards were some of the more obvious instances where this revolution affected every aspect of private and commercial life.
To appreciate how this involved cryptology, contrast what is involved when a customer makes a noncash purchase in person with what is involved in a similar transaction in e-commerce. For a direct purchase, the merchant routinely asks for some photo identification, usually a driver’s license, to verify the customer’s identity. Neither party is ordinarily concerned with secrecy; both are vitally concerned with other aspects of information integrity. Next, consider an analogous transaction over the Internet. The merchant must still verify the customer’s identity, even though they may be separated by thousands of miles, and the customer must still be assured that he will only be charged the agreed amount. However, there is a whole gamut of new concerns. The customer must be assured that information he communicates to the merchant is confidential and protected from interception by others. And while the merchant retains the customer’s signature as material proof of a direct transaction, he has only a string of 0s and 1s on a hard disk following an e-commerce transaction. The merchant must be confident that this “information” will suffice for him to collect payment, as well as protect him should the customer later disavow the transaction or claim that it was for a different amount. All of these concerns, and more, have to be met before the simplest e-commerce transactions can be made securely. As a result, cryptology has been extended far beyond its original function of providing secrecy.
The conduct of commerce, affairs of state, military actions, and personal affairs all depend on the existence of generally accepted means of authenticating identity, authority, ownership, license, signature, notarization, date of action, receipt, and so on. In the past these have depended almost entirely on documents, and on protocols for the creation of those documents, for authentication. Society has evolved and adopted a complex set of legal and forensic procedures, depending almost entirely on the physical evidence intrinsic to the documents themselves, to resolve disputes over authenticity. In the information age, however, possession, control, transfer, or access to real assets is frequently based on electronic information, and a license to use, modify, or disseminate valuable information itself is similarly determined. Thus, it is essential that internal evidence be present in the information itself—since that is the only thing available. Modern cryptology, therefore, must provide every function presently served by documents—public and private. In fact, it frequently must do more. When someone mails a document by certified mail with a request for a delivery receipt, the receipt only proves that an envelope was delivered; it says nothing about the contents. Digital certificates of origination and digital receipts, though, are inextricably linked to each electronic document. Many other functions, such as signatures, are also much more demanding in a digital setting. In June 2000 the U.S. Congress gave digital signatures the same legal status as written signatures—the first such legislation in the world.
In classical cryptology the participants trust each other but not outsiders; typical examples include diplomatic communications and military commands. In business and personal transactions, though, the situation is almost the opposite, as the participants may have various motives for cheating. For example, the cheater may wish to impersonate some other participant, to eavesdrop on communications between other participants, or to intercept and modify information being communicated between other users. The cheater may be an insider who wishes to disavow communications he actually originated or to claim to have received messages from other participants who did not send them. He may wish to enlarge his license to gain access to information to which he is not supposed to have access or to alter the license of others. He may wish simply to subvert the system to deny services to others or to cause other users to reject as fraudulent information that is in fact legitimate. Therefore, modern cryptology must also prevent every form of cheating or, failing that, detect cheating in information-based systems where the means for cheating depends only on tampering with electronic information.
At the beginning of the 1990s, most people would likely have been hard-pressed to say where cryptology had an impact on their day-to-day lives. Today, people who have purchased merchandise over the Internet are familiar with warnings that they are about to exchange information over a secure link. When a warning appears alerting consumers that a merchant’s authentication has either expired or is not working, they are aware that this is a warning to proceed at their own risk in providing personal information, such as credit card numbers. Only a few consumers are aware, however, that behind this exchange of authentications is a 128-bit cryptography key that has been in common use around the world for transactions over the Internet since it was approved for export by the U.S. government in 2000, replacing an earlier 40-bit key that had been made insecure by the growing power of computers to test it. The 128-bit key offers “strong encryption” that protects Internet transactions against almost any threat; nevertheless, some Web browsers will support an even stronger 256-bit encryption key, which offers a much stronger level of protection required by many governments for top-secret documents.
Cryptology, indeed, has long been a part of modern daily life. In particular, electronic banking and various financial, medical, and legal databases depend on cryptology for security. One example is the personal identity number (PIN), a coded identification that must be entered into an automated teller machine (ATM) along with a bankcard to corroborate that the card is being used by an authorized bearer. The PIN may be stored in an encrypted form (as a cipher) either in the bank’s computers or on the card itself. The transformation used in this type of cryptography is called one-way; i.e., it is easy to compute a cipher when given the bank’s key and the customer’s PIN, but it is computationally infeasible to compute the plaintext PIN from the cipher even when the key is known. This protects the cardholder from being impersonated by someone who has access to the bank’s computer files. Similarly, communications between the ATM and the bank’s central computer are encrypted to prevent a would-be thief from tapping into the phone lines and recording the signals sent to the ATM to authorize the dispensing of cash in response to a legitimate user request and then later feeding the same signals to the ATM repeatedly to deceive it into dispensing money illegitimately from the customer’s account.
A novel application that involves all aspects of cryptography is the “smart” credit card, which has a microprocessor built into the card itself. The user must corroborate his identity to the card each time a transaction is made, in much the same way that a PIN is used with an ATM. The card and the card reader execute a sequence of encrypted sign/countersign-like exchanges to verify that each is dealing with a legitimate counterpart. Once this has been established, the transaction itself is carried out in encrypted form to prevent anyone, including the cardholder or the merchant whose card reader is involved, from eavesdropping on the exchange and then later impersonating either party to defraud the system. This elaborate protocol is carried out in a way that is invisible to the user, except for the necessity of entering a PIN to initiate the transaction. Smart cards are in widespread use throughout Europe, much more so than the “dumb” plastic cards common in the United States. The Advanced Encryption Standard (AES; see History of cryptology), approved as a secure communications standard by the U.S. National Institute of Standards and Technology (NIST) in 2000, is compatible with implementation in smart cards, unlike its predecessor, the Data Encryption Standard (DES).

Cryptography

Cryptography, as defined in the introduction to this article, is the science of transforming information into a form that is impossible or infeasible to duplicate or undo without knowledge of a secret key. Cryptographic systems are generically classified (1) by the mathematical operations through which the information (called the “plaintext”) is concealed using the encryption key—namely, transposition, substitution, or product ciphers in which two such operations are cascaded; (2) according to whether the transmitter and receiver use the same key (symmetric [single-key] cryptosystem) or different keys (asymmetric [two-key or public-key] cryptosystem); and (3) by whether they produce block or stream ciphers. These three types of system are described in turn below.

Cipher systems

The easiest way to describe the techniques on which cryptography depends is first to examine some simple cipher systems and then abstract from these examples features that apply to more complex systems. There are two basic kinds of mathematical operations used in cipher systems: transpositions and substitutions. Transpositions rearrange the symbols in the plaintext without changing the symbols themselves. Substitutions replace plaintext elements (symbols, pairs of symbols, etc.) with other symbols or groups of symbols without changing the sequence in which they occur.

TRANSPOSITION CIPHERS

In manual systems transpositions are generally carried out with the aid of an easily remembered mnemonic. For example, a popular schoolboy cipher is the “rail fence,” in which letters of the plaintext are written alternating between rows and the rows are then read sequentially to give the cipher. In a depth-two rail fence (two rows) the message WE ARE DISCOVERED SAVE YOURSELF would be written
Simple frequency counts on the ciphertext would reveal to the cryptanalyst that letters occur with precisely the same frequency in the cipher as in an average plaintext and, hence, that a simple rearrangement of the letters is probable.
The rail fence is the simplest example of a class of transposition ciphers, known as route ciphers, that enjoyed considerable popularity in the early history of cryptology. In general, the elements of the plaintext (usually single letters) are written in a prearranged order (route) into a geometric array (matrix)—typically a rectangle—agreed upon in advance by the transmitter and receiver and then read off by following another prescribed route through the matrix to produce the cipher. The key in a route cipher consists of keeping secret the geometric array, the starting point, and the routes. Clearly, both the matrix and the routes can be much more complex than in this example; but even so, they provide little security. One form of transposition (permutation) that was widely used depends on an easily remembered key word for identifying the route in which the columns of a rectangular matrix are to be read. For example, using the key word AUTHOR and ordering the columns by the lexicographic order of the letters in the key word
In decrypting a route cipher, the receiver enters the ciphertext symbols into the agreed-upon matrix according to the encryption route and then reads the plaintext according to the original order of entry. A significant improvement in cryptosecurity can be achieved by reencrypting the cipher obtained from one transposition with another transposition. Because the result (product) of two transpositions is also a transposition, the effect of multiple transpositions is to define a complex route in the matrix, which in itself would be difficult to describe by any simple mnemonic. (See Product ciphers, below.)
In the same class also fall systems that make use of perforated cardboard matrices called grilles; descriptions of such systems can be found in most older books on cryptography. In contemporary cryptography, transpositions serve principally as one of several encryption steps in forming a compound or product cipher.

SUBSTITUTION CIPHERS

In substitution ciphers, units of the plaintext (generally single letters or pairs of letters) are replaced with other symbols or groups of symbols, which need not be the same as those used in the plaintext. For instance, in Sir Arthur Conan Doyle’s Adventure of the Dancing Men (1903), Sherlock Holmes solves a monoalphabetic substitution cipher in which the ciphertext symbols are stick figures of a human in various dancelike poses.
The simplest of all substitution ciphers are those in which the cipher alphabet is merely a cyclical shift of the plaintext alphabet. Of these, the best-known is the Caesar cipher, used byJulius Caesar, in which A is encrypted as D, B as E, and so forth. As many a schoolboy has discovered to his embarrassment, cyclical-shift substitution ciphers are not secure. And as is pointed out in the section Cryptanalysis, neither is any other monoalphabetic substitution cipher in which a given plaintext symbol is always encrypted into the same ciphertext symbol. Because of the redundancy of the English language, only about 25 symbols of ciphertext are required to permit the cryptanalysis of monoalphabetic substitution ciphers, which makes them a popular source for recreational cryptograms. The explanation for this weakness is that the frequency distributions of symbols in the plaintext and in the ciphertext are identical, only the symbols having been relabeled. In fact, any structure or pattern in the plaintext is preserved intact in the ciphertext, so that the cryptanalyst’s task is an easy one.
There are two main approaches that have been employed with substitution ciphers to lessen the extent to which structure in the plaintext—primarily single-letter frequencies—survives in the ciphertext. One approach is to encrypt elements of plaintext consisting of two or more symbols; e.g., digraphs and trigraphs. The other is to use several cipher alphabets. When this approach of polyalphabetic substitution is carried to its limit, it results in onetime keys, or pads.

PLAYFAIR CIPHERS

In cryptosystems for manually encrypting units of plaintext made up of more than a single letter, only digraphs were ever used. By treating digraphs in the plaintext as units rather than as single letters, the extent to which the raw frequency distribution survives the encryption process can be lessened but not eliminated, as letter pairs are themselves highly correlated. The best-known digraph substitution cipher is the Playfair, invented by Sir Charles Wheatstone but championed at the British Foreign Office by Lyon Playfair, the first Baron Playfair of St. Andrews. Below is an example of a Playfair cipher, solved by Lord Peter Wimsey in Dorothy L. Sayers’s Have His Carcase (1932). Here, the mnemonic aid used to carry out the encryption is a 5 × 5-square matrix containing the letters of the alphabet (I and J are treated as the same letter). A key word, MONARCHY in this example, is filled in first, and the remaining unused letters of the alphabet are entered in their lexicographic order:
Plaintext digraphs are encrypted with the matrix by first locating the two plaintext letters in the matrix. They are (1) in different rows and columns; (2) in the same row; (3) in the same column; or (4) alike. The corresponding encryption (replacement) rules are the following:
  1. When the two letters are in different rows and columns, each is replaced by the letter that is in the same row but in the other column; i.e., to encrypt WE, W is replaced by U and E by G.
  2. When A and R are in the same row, A is encrypted as R and R (reading the row cyclically) as M.
  3. When I and S are in the same column, I is encrypted as S and S as X.
  4. When a double letter occurs, a spurious symbol, say Q, is introduced so that the MM in SUMMER is encrypted as NL for MQ and CL for ME.
  5. An X is appended to the end of the plaintext if necessary to give the plaintext an even number of letters.
Encrypting the familiar plaintext example using Sayers’s Playfair array yields:
If the frequency distribution information were totally concealed in the encryption process, the ciphertext plot of letter frequencies in Playfair ciphers would be flat. It is not. The deviation from this ideal is a measure of the tendency of some letter pairs to occur more frequently than others and of the Playfair’s row-and-column correlation of symbols in the ciphertext—the essential structure exploited by a cryptanalyst in solving Playfair ciphers. The loss of a significant part of the plaintext frequency distribution, however, makes a Playfair cipher harder to cryptanalyze than a monoalphabetic cipher.

VIGENÈRE CIPHERS

The other approach to concealing plaintext structure in the ciphertext involves using several different monoalphabetic substitution ciphers rather than just one; the key specifies which particular substitution is to be employed for encrypting each plaintext symbol. The resulting ciphers, known generically as polyalphabetics, have a long history of usage. The systems differ mainly in the way in which the key is used to choose among the collection of monoalphabetic substitution rules.
The best-known polyalphabetics are the simple Vigenère ciphers, named for the 16th-century French cryptographer Blaise de Vigenère. For many years this type of cipher was thought to be impregnable and was known as le chiffre indéchiffrable, literally “the unbreakable cipher.” The procedure for encrypting and decrypting Vigenère ciphers is illustrated in the figure.
In the simplest systems of the Vigenère type, the key is a word or phrase that is repeated as many times as required to encipher a message. If the key is DECEPTIVE and the message is WE ARE DISCOVERED SAVE YOURSELF, then the resulting cipher will be
The graph shows the extent to which the raw frequency of occurrence pattern is obscured by encrypting the text of this article using the repeating key DECEPTIVE. Nevertheless, in 1861Friedrich W. Kasiski, formerly a German army officer and cryptanalyst, published a solution of repeated-key Vigenère ciphers based on the fact that identical pairings of message and key symbols generate the same cipher symbols. Cryptanalysts look for precisely such repetitions. In the example given above, the group VTW appears twice, separated by six letters, suggesting that the key (i.e., word) length is either three or nine. Consequently, the cryptanalyst would partition the cipher symbols into three and nine monoalphabets and attempt to solve each of these as a simple substitution cipher. With sufficient ciphertext, it would be easy to solve for the unknown key word.
The periodicity of a repeating key exploited by Kasiski can be eliminated by means of a running-key Vigenère cipher. Such a cipher is produced when a nonrepeating text is used for the key. Vigenère actually proposed concatenating the plaintext itself to follow a secret key word in order to provide a running key in what is known as an autokey.
Even though running-key or autokey ciphers eliminate periodicity, two methods exist to cryptanalyze them. In one, the cryptanalyst proceeds under the assumption that both the ciphertext and the key share the same frequency distribution of symbols and applies statistical analysis. For example, E occurs in English plaintext with a frequency of 0.0169, and T occurs only half as often. The cryptanalyst would, of course, need a much larger segment of ciphertext to solve a running-key Vigenère cipher, but the basic principle is essentially the same as before—i.e., the recurrence of like events yields identical effects in the ciphertext. The second method of solving running-key ciphers is commonly known as the probable-word method. In this approach, words that are thought most likely to occur in the text are subtracted from the cipher. For example, suppose that an encrypted message to President Jefferson Davis of the Confederate States of America was intercepted. Based on a statistical analysis of the letter frequencies in the ciphertext, and the South’s encryption habits, it appears to employ a running-key Vigenère cipher. A reasonable choice for a probable word in the plaintext might be “PRESIDENT.” For simplicity a space will be encoded as a “0.” PRESIDENT would then be encoded—not encrypted—as “16, 18, 5, 19, 9, 4, 5, 14, 20” using the rule A = 1, B = 2, and so forth. Now these nine numbers are added modulo 27 (for the 26 letters plus a space symbol) to each successive block of nine symbols of ciphertext—shifting one letter each time to form a new block. Almost all such additions will produce random-like groups of nine symbols as a result, but some may produce a block that contains meaningful English fragments. These fragments can then be extended with either of the two techniques described above. If provided with enough ciphertext, the cryptanalyst can ultimately decrypt the cipher. What is important to bear in mind here is that the redundancy of the English language is high enough that the amount of information conveyed by every ciphertext component is greater than the rate at which equivocation (i.e., the uncertainty about the plaintext that the cryptanalyst must resolve to cryptanalyze the cipher) is introduced by the running key. In principle, when the equivocation is reduced to zero, the cipher can be solved. The number of symbols needed to reach this point is called the unicity distance—and is only about 25 symbols, on average, for simple substitution ciphers.

VERNAM-VIGENÈRE CIPHERS

In 1918 Gilbert S. Vernam, an engineer for the American Telephone & Telegraph Company (AT&T), introduced the most important key variant to the Vigenère system. At that time all messages transmitted over AT&T’s teleprinter system were encoded in the Baudot Code, a binary code in which a combination of marks and spaces represents a letter, number, or other symbol. Vernam suggested a means of introducing equivocation at the same rate at which it was reduced by redundancy among symbols of the message, thereby safeguarding communications against cryptanalytic attack. He saw that periodicity (as well as frequency information and intersymbol correlation), on which earlier methods of decryption of different Vigenère systems had relied, could be eliminated if a random series of marks and spaces (a running key) were mingled with the message during encryption to produce what is known as a stream or streaming cipher.
There was one serious weakness in Vernam’s system, however. It required one key symbol for each message symbol, which meant that communicants would have to exchange an impractically large key in advance—i.e., they had to securely exchange a key as large as the message they would eventually send. The key itself consisted of a punched paper tape that could be read automatically while symbols were typed at the teletypewriter keyboard and encrypted for transmission. This operation was performed in reverse using a copy of the paper tape at the receiving teletypewriter to decrypt the cipher. Vernam initially believed that a short random key could safely be reused many times, thus justifying the effort to deliver such a large key, but reuse of the key turned out to be vulnerable to attack by methods of the type devised by Kasiski. Vernam offered an alternative solution: a key generated by combining two shorter key tapes ofm and n binary digits, or bits, where m and n share no common factor other than 1 (they are relatively prime). A bit stream so computed does not repeat until mn bits of key have been produced. This version of the Vernam cipher system was adopted and employed by the U.S. Army until Major Joseph O. Mauborgne of the Army Signal Corps demonstrated during World War I that a cipher constructed from a key produced by linearly combining two or more short tapes could be decrypted by methods of the sort employed to cryptanalyze running-key ciphers. Mauborgne’s work led to the realization that neither the repeating single-key nor the two-tapeVernam-Vigenère cipher system was cryptosecure. Of far greater consequence to modern cryptology—in fact, an idea that remains its cornerstone—was the conclusion drawn by Mauborgne and William F. Friedman that the only type of cryptosystem that is unconditionally secure uses a random onetime key. The proof of this, however, was provided almost 30 years later by another AT&T researcher, Claude Shannon, the father of modern information theory.
In a streaming cipher the key is incoherent—i.e., the uncertainty that the cryptanalyst has about each successive key symbol must be no less than the average information content of a message symbol. The dotted curve in the figure indicates that the raw frequency of occurrence pattern is lost when the draft text of this article is encrypted with a random onetime key. The same would be true if digraph or trigraph frequencies were plotted for a sufficiently long ciphertext. In other words, the system is unconditionally secure, not because of any failure on the part of the cryptanalyst to find the right cryptanalytic technique but rather because he is faced with an irresolvable number of choices for the key or plaintext message.

PRODUCT CIPHERS

In the discussion of transposition ciphers it was pointed out that by combining two or more simple transpositions, a more secure encryption may result. In the days of manual cryptography this was a useful device for the cryptographer, and in fact double transposition or product ciphers on key word-based rectangular matrices were widely used. There was also some use of a class of product ciphers known as fractionation systems, wherein a substitution was first made from symbols in the plaintext to multiple symbols (usually pairs, in which case the cipher is called a biliteral cipher) in the ciphertext, which was then encrypted by a final transposition, known as superencryption. One of the most famous field ciphers of all time was a fractionation system, the ADFGVX cipher employed by the German army during World War I. This system used a 6 × 6 matrix to substitution-encrypt the 26 letters and 10 digits into pairs of the symbols A, D, F, G, V, and X. The resulting biliteral cipher was then written into a rectangular array and route encrypted by reading the columns in the order indicated by a key word, as illustrated in thefigure.
The great French cryptanalyst Georges J. Painvin succeeded in cryptanalyzing critical ADFGVX ciphers in 1918, with devastating effect for the German army in the battle for Paris.

Key cryptosystems

SINGLE-KEY CRYPTOGRAPHY

Single-key cryptography is limited in practice by what is known as the key distribution problem. Since all participants must possess the same secret key, if they are physically separated—as is usually the case—there is the problem of how they get the key in the first place. Diplomatic and military organizations traditionally use couriers to distribute keys for the highest-level communications systems, which are then used to superencrypt and distribute keys for lower-level systems. This is impractical, though, for most business and private needs. In addition, key holders are compelled to trust each other unconditionally to protect the keys in their possession and not to misuse them. Again, while this may be a tolerable condition in diplomatic and military organizations, it is almost never acceptable in the commercial realm.
Another key distribution problem is the sheer number of keys required for flexible, secure communications among even a modest number of users. While only a single key is needed for secure communication between two parties, every potential pair of participants in a larger group needs a unique key. To illustrate this point, consider an organization with only 1,000 users: each individual would need a different private key for each of the other 999 users. Such a system would require 499,500 different keys in all, with each user having to protect 999 keys. The number of different keys increases in proportion to the square of the number of users. Secure distribution for so many keys is simply insolvable, as are the demands on the users for the secure storage of their keys. In other words, symmetric key cryptography is impractical in a network in which all participants are equals in all respects. One “solution” is to create a trusted authority—unconditionally trusted by all users—with whom each user can communicate securely to generate and distribute temporary session keys as needed. Each user then has only to protect one key, while the burden for the protection of all of the keys in the network is shifted to the central authority.

TWO-KEY CRYPTOGRAPHY

PUBLIC-KEY CRYPTOGRAPHY

In 1976, in one of the most inspired insights in the history of cryptology, Sun Microsystems, Inc., computer engineer Whitfield Diffie and Stanford University electrical engineer Martin Hellmanrealized that the key distribution problem could be almost completely solved if a cryptosystem, T(and perhaps an inverse system, T′), could be devised that used two keys and satisfied the following conditions:
  1. It must be easy for the cryptographer to calculate a matched pair of keys, e (encryption) and d(decryption), for which TeT′d = I. Although not essential, it is desirable that T′dTe = I and thatT = T′. Since most of the systems devised to meet points 1–4 satisfy these conditions as well, we will assume they hold hereafter—but that is not necessary.
  2. The encryption and decryption operation, T, should be (computationally) easy to carry out.
  3. At least one of the keys must be computationally infeasible for the cryptanalyst to recover even when he knows T, the other key, and arbitrarily many matching plaintext and ciphertext pairs.
  4. It should not be computationally feasible to recover x given y, where y = Tk(x) for almost all keys k and messages x.
Given such a system, Diffie and Hellman proposed that each user keep his decryption key secret and publish his encryption key in a public directory. Secrecy was not required, either in distributing or in storing this directory of “public” keys. Anyone wishing to communicate privately with a user whose key is in the directory only has to look up the recipient’s public key to encrypt a message that only the intended receiver can decrypt. The total number of keys involved is just twice the number of users, with each user having a key in the public directory and his own secret key, which he must protect in his own self-interest. Obviously, the public directory must be authenticated, otherwise A could be tricked into communicating with C when he thinks he is communicating with B simply by substituting C’s key for B’s in A’s copy of the directory. Since they were focused on the key distribution problem, Diffie and Hellman called their discoverypublic-key cryptography. This was the first discussion of two-key cryptography in the open literature. However, Admiral Bobby Inman, while director of the U.S. National Security Agency (NSA) from 1977 to 1981, revealed that two-key cryptography had been known to the agency almost a decade earlier, having been discovered by James Ellis, Clifford Cocks, and Malcolm Williamson at the British Government Code Headquarters (GCHQ).
In this system, ciphers created with a secret key can be decrypted by anyone using the corresponding public key—thereby providing a means to identify the originator at the expense of completely giving up secrecy. Ciphers generated using the public key can only be decrypted by users holding the secret key, not by others holding the public key—however, the secret-key holder receives no information concerning the sender. In other words, the system provides secrecy at the expense of completely giving up any capability of authentication. What Diffie and Hellman had done was to separate the secrecy channel from the authentication channel—a striking example of the sum of the parts being greater than the whole. Single-key cryptography is called symmetric for obvious reasons. A cryptosystem satisfying conditions 1–4 above is called asymmetric for equally obvious reasons. There are symmetric cryptosystems in which the encryption and decryption keys are not the same—for example, matrix transforms of the text in which one key is a nonsingular (invertible) matrix and the other its inverse. Even though this is a two-key cryptosystem, since it is easy to calculate the inverse to a non-singular matrix, it does not satisfy condition 3 and is not considered to be asymmetric.
Since in an asymmetric cryptosystem each user has a secrecy channel from every other user to him (using his public key) and an authentication channel from him to all other users (using his secret key), it is possible to achieve both secrecy and authentication using superencryption. Say Awishes to communicate a message in secret to B, but B wants to be sure the message was sent byA. A first encrypts the message with his secret key and then superencrypts the resulting cipher with B’s public key. The resulting outer cipher can only be decrypted by B, thus guaranteeing to Athat only B can recover the inner cipher. When B opens the inner cipher using A’s public key he is certain the message came from someone knowing A’s key, presumably A. Simple as it is, this protocol is a paradigm for many contemporary applications.
Cryptographers have constructed several cryptographic schemes of this sort by starting with a “hard” mathematical problem—such as factoring a number that is the product of two very large primes—and attempting to make the cryptanalysis of the scheme be equivalent to solving the hard problem. If this can be done, the cryptosecurity of the scheme will be at least as good as the underlying mathematical problem is hard to solve. This has not been proven for any of the candidate schemes thus far, although it is believed to hold in each instance.
However, a simple and secure proof of identity is possible based on such computational asymmetry. A user first secretly selects two large primes and then openly publishes their product. Although it is easy to compute a modular square root (a number whose square leaves a designated remainder when divided by the product) if the prime factors are known, it is just as hard as factoring (in fact equivalent to factoring) the product if the primes are unknown. A user can therefore prove his identity, i.e., that he knows the original primes, by demonstrating that he can extract modular square roots. The user can be confident that no one can impersonate him since to do so they would have to be able to factor his product. There are some subtleties to the protocol that must be observed, but this illustrates how modern computational cryptography depends on hard problems.

SECRET-SHARING

To understand public-key cryptography fully, one must first understand the essentials of one of the basic tools in contemporary cryptology: secret-sharing. There is only one way to design systems whose overall reliability must be greater than that of some critical components—as is the case for aircraft, nuclear weapons, and communications systems—and that is by the appropriate use of redundancy so the system can continue to function even though some components fail. The same is true for information-based systems in which the probability of the security functions being realized must be greater than the probability that some of the participants will not cheat. Secret-sharing, which requires a combination of information held by each participant in order to decipher the key, is a means to enforce concurrence of several participants in the expectation that it is less likely that many will cheat than that one will.
The RSA cryptoalgorithm described in the next section is a two-out-of-two secret-sharing scheme in which each key individually provides no information. Other security functions, such as digital notarization or certification of origination or receipt, depend on more complex sharing of information related to a concealed secret.

RSA ENCRYPTION

The best-known public-key scheme is the Rivest–Shamir–Adleman (RSA) cryptoalgorithm. In this system a user secretly chooses a pair of prime numbers p and q so large that factoring the product n = pq is well beyond projected computing capabilities for the lifetime of the ciphers. At the beginning of the 21st century, U.S. government security standards called for the modulus to be 1,024 bits in size—i.e., p and q each were to be about 155 decimal digits in size, with nroughly a 310-digit number. However, over the following decade, as processor speeds grew and computing techniques became more sophisticated, numbers approaching this size were factored, making it likely that, sooner rather than later, 1,024-bit moduli would no longer be safe, so the U.S. government recommended shifting in 2011 to 2,048-bit moduli.
Having chosen p and q, the user selects an arbitrary integer e less than n and relatively prime top − 1 and q − 1, that is, so that 1 is the only factor in common between e and the product (p − 1)(q − 1). This assures that there is another number d for which the product ed will leave a remainder of 1 when divided by the least common multiple of p − 1 and q − 1. With knowledge of p and q, the number d can easily be calculated using the Euclidean algorithm. If one does not know p and q, it is equally difficult to find either e or d given the other as to factor n, which is the basis for the cryptosecurity of the RSA algorithm.
We will use the labels d and e to denote the function to which a key is put, but as keys are completely interchangeable, this is only a convenience for exposition. To implement a secrecy channel using the standard two-key version of the RSA cryptosystem, user A would publish e andn in an authenticated public directory but keep d secret. Anyone wishing to send a private message to A would encode it into numbers less than n and then encrypt it using a special formula based on e and n. A can decrypt such a message based on knowing d, but the presumption—and evidence thus far—is that for almost all ciphers no one else can decrypt the message unless he can also factor n.
Similarly, to implement an authentication channel, A would publish d and n and keep e secret. In the simplest use of this channel for identity verification, B can verify that he is in communication with A by looking in the directory to find A’s decryption key d and sending him a message to be encrypted. If he gets back a cipher that decrypts to his challenge message using d to decrypt it, he will know that it was in all probability created by someone knowing e and hence that the other communicant is probably A. Digitally signing a message is a more complex operation and requires a cryptosecure “hashing” function. This is a publicly known function that maps any message into a smaller message—called a digest—in which each bit of the digest is dependent on every bit of the message in such a way that changing even one bit in the message is apt to change, in a cryptosecure way, half of the bits in the digest. By cryptosecure is meant that it is computationally infeasible for anyone to find a message that will produce a preassigned digest and equally hard to find another message with the same digest as a known one. To sign a message—which may not even need to be kept secret—A encrypts the digest with the secret e, which he appends to the message. Anyone can then decrypt the message using the public key dto recover the digest, which he can also compute independently from the message. If the two agree, he must conclude that A originated the cipher, since only A knew e and hence could have encrypted the message.
Thus far, all proposed two-key cryptosystems exact a very high price for the separation of the privacy or secrecy channel from the authentication or signature channel. The greatly increased amount of computation involved in the asymmetric encryption/decryption process significantly cuts the channel capacity (bits per second of message information communicated). As a result, the main application of two-key cryptography is in hybrid systems. In such a system a two-key algorithm is used for authentication and digital signatures or to exchange a randomly generated session key to be used with a single-key algorithm at high speed for the main communication. At the end of the session this key is discarded.

Block and stream ciphers

In general, cipher systems transform fixed-size pieces of plaintext into ciphertext. In older manual systems these pieces were usually single letters or characters—or occasionally, as in the Playfair cipher, digraphs, since this was as large a unit as could feasibly be encrypted and decrypted by hand. Systems that operated on trigrams or larger groups of letters were proposed and understood to be potentially more secure, but they were never implemented because of the difficulty in manual encryption and decryption. In modern single-key cryptography the units of information are often as large as 64 bits, or about 131/2 alphabetic characters, whereas two-key cryptography based on the RSA algorithm appears to have settled on 1,024 to 2,048 bits, or between 310 and 620 alphabetic characters, as the unit of encryption.
A block cipher breaks the plaintext into blocks of the same size for encryption using a common key: the block size for a Playfair cipher is two letters, and for the DES (described in the sectionHistory of cryptology: The Data Encryption Standard and the Advanced Encryption Standard) used in electronic codebook mode it is 64 bits of binary-encoded plaintext. Although a block could consist of a single symbol, normally it is larger.
A stream cipher also breaks the plaintext into units, normally of a single character, and then encrypts the ith unit of the plaintext with the ith unit of a key stream. Vernam encryption with a onetime key is an example of such a system, as are rotor cipher machines and the DES used in the output feedback mode (in which the ciphertext from one encryption is fed back in as the plaintext for the next encryption) to generate a key stream. Stream ciphers depend on the receiver’s using precisely the same part of the key stream to decrypt the cipher that was employed to encrypt the plaintext. They thus require that the transmitter’s and receiver’s key-stream generators be synchronized. This means that they must be synchronized initially and stay in sync thereafter, or else the cipher will be decrypted into a garbled form until synchrony can be reestablished. This latter property of self-synchronizing cipher systems results in what is known as error propagation, an important parameter in any stream-cipher system.

Cryptanalysis

Cryptanalysis, as defined at the beginning of this article, is the art of deciphering or even forging communications that are secured by cryptography. History abounds with examples of the seriousness of the cryptographer’s failure and the cryptanalyst’s success. In World War II theBattle of Midway, which marked the turning point of the naval war in the Pacific, was won by the United States largely because cryptanalysis had provided Admiral Chester W. Nimitz with information about the Japanese diversionary attack on the Aleutian Islands and about the Japanese order of attack on Midway. Another famous example of cryptanalytic success was the deciphering by the British during World War I of a telegram from the German foreign minister, Arthur Zimmermann, to the German minister in Mexico City, Heinrich von Eckardt, laying out a plan to reward Mexico for entering the war as an ally of Germany. American newspapers published the text (without mentioning the British role in intercepting and decoding the telegram), and the news stories, combined with German submarine attacks on American ships, accelerated a shift in public sentiment for U.S. entry into the war on the side of the Allies. In 1982, during a debate over the Falkland Islands War, a member of Parliament, in a now-famous gaffe, revealed that the British were reading Argentine diplomatic ciphers with as much ease as Argentine code clerks.

Basic aspects

While cryptography is clearly a science with well-established analytic and synthetic principles, cryptanalysis in the past was as much an art as it was a science. The reason is that success in cryptanalyzing a cipher is as often as not a product of flashes of inspiration, gamelike intuition, and, most important, recognition by the cryptanalyst of pattern or structure, at almost the subliminal level, in the cipher. It is easy to state and demonstrate the principles on which the scientific part of cryptanalysis depends, but it is nearly impossible to convey an appreciation of the art with which the principles are applied. In present-day cryptanalysis, however, mathematics and enormous amounts of computing power are the mainstays.
Cryptanalysis of single-key cryptosystems (described in the section Cryptography: Key cryptosystems) depends on one simple fact—namely, that traces of structure or pattern in the plaintext may survive encryption and be discernible in the ciphertext. Take, for example, the following: in a monoalphabetic substitution cipher (in which each letter is simply replaced by another letter), the frequency with which letters occur in the plaintext alphabet and in the ciphertext alphabet is identical. The cryptanalyst can use this fact in two ways: first, to recognize that he is faced with a monoalphabetic substitution cipher and, second, to aid him in selecting the likeliest equivalences of letters to be tried. The table shows the number of occurrences of each letter in the text of this article, which approximates the raw frequency distribution for most technical material. The following cipher is an encryption of the first sentence of this paragraph (minus the parenthetical clause) using a monoalphabetic substitution:
Letter frequency distribution for a sample English text
letternumber of occurrencesfrequencyletternumber of occurrencesfrequency
E8,915.127Y1,891.027
T6,828.097U1,684.024
I5,260.075M1,675.024
A5,161.073F1,488.021
O4,814.068B1,173.017
N4,774.067G1,113.016
S4,700.067W914.013
R4,517.064V597.008
H3,452.049K548.008
C3,188.045X330.005
L2,810.040Q132.002
D2,161.031Z65.001
P2,082.030J56.001
UFMDHQAQTMGRG BX GRAZTW PWM
UFMDHBGMGHWOG VWDWAVG BA BAW
GRODTW XQUH AQOWTM HCQH HFQUWG
BX GHFIUHIFW BF DQHHWFA RA HCW
DTQRAHWLH OQM GIFJRJW WAUFMDHRBA
QAV SW VRGUWFARSTW RA HCW
URDCWFHWLH.
W occurs 21 times in the cipher, H occurs 18, and so on. Even the rankest amateur, using the frequency data in the table, should have no difficulty in recovering the plaintext and all but four symbols of the key in this case.
It is possible to conceal information about raw frequency of occurrence by providing multiple cipher symbols for each plaintext letter in proportion to the relative frequency of occurrence of the letter—i.e., twice as many symbols for E as for S, and so on. The collection of cipher symbols representing a given plaintext letter are called homophones. If the homophones are chosen randomly and with uniform probability when used, the cipher symbols will all occur (on average) equally often in the ciphertext. The great German mathematician Carl Friedrich Gauss (1777–1855) believed that he had devised an unbreakable cipher by introducing homophones. Unfortunately for Gauss and other cryptographers, such is not the case, since there are many other persistent patterns in the plaintext that may partially or wholly survive encryption. Digraphs, for example, show a strong frequency distribution: TH occurring most often, about 20 times as frequently as HT, and so forth. With the use of tables of digraph frequencies that partially survive even homophonic substitution, it is still an easy matter to cryptanalyze a random substitution cipher, though the amount of ciphertext needed grows to a few hundred instead of a few tens of letters.

Types of cryptanalysis

There are three generic types of cryptanalysis, characterized by what the cryptanalyst knows: (1) ciphertext only, (2) known ciphertext/plaintext pairs, and (3) chosen plaintext or chosen ciphertext. In the discussion of the preceding paragraphs, the cryptanalyst knows only the ciphertext and general structural information about the plaintext. Often the cryptanalyst either will know some of the plaintext or will be able to guess at, and exploit, a likely element of the text, such as a letter beginning with “Dear Sir” or a computer session starting with “LOG IN.” The last category represents the most favourable situation for the cryptanalyst, in which he can cause either the transmitter to encrypt a plaintext of his choice or the receiver to decrypt a ciphertext that he chose. Of course, for single-key cryptography there is no distinction between chosen plaintext and chosen ciphertext, but in two-key cryptography it is possible for one of the encryption or decryption functions to be secure against chosen input while the other is vulnerable.
One measure of the security of a cryptosystem is its resistance to standard cryptanalysis; another is its work function—i.e., the amount of computational effort required to search the key space exhaustively. The first can be thought of as an attempt to find an overlooked back door into the system, the other as a brute-force frontal attack. Assume that the analyst has only ciphertext available and, with no loss of generality, that it is a block cipher (described in the sectionCryptography: Block and stream ciphers). He could systematically begin decrypting a block of the cipher with one key after another until a block of meaningful text was output (although it would not necessarily be a block of the original plaintext). He would then try that key on the next block of cipher, very much like the technique devised by Friedrich Kasiski to extend a partially recovered key from the probable plaintext attack on a repeated-key Vigenère cipher. If the cryptanalyst has the time and resources to try every key, he will eventually find the right one. Clearly, no cryptosystem can be more secure than its work function.
The 40-bit key cipher systems approved for use in the 1990s were eventually made insecure, as is mentioned in the section Cryptology: Cryptology in private and commercial life. There are 24040-bit keys possible—very close to 1012—which is the work function of these systems. Most personal computers (PCs) at the end of the 20th century could execute roughly 1,000 MIPS (millions of instructions per second), or 3.6 × 1012 per hour. Testing a key might involve many instructions, but even so, a single PC at that time could search a 240-key space in a matter of hours. Alternatively, the key space could be partitioned and the search carried out by multiple machines, producing a solution in minutes or even seconds. Clearly, by the year 2000, 40-bit keys were not secure by any standard, a situation that brought on the shift to the 128-bit key.
Because of its reliance on “hard” mathematical problems as a basis for cryptoalgorithms and because one of the keys is publicly exposed, two-key cryptography has led to a new type of cryptanalysis that is virtually indistinguishable from research in any other area of computational mathematics. Unlike the ciphertext attacks or ciphertext/plaintext pair attacks in single-key cryptosystems, this sort of cryptanalysis is aimed at breaking the cryptosystem by analysis that can be carried out based only on a knowledge of the system itself. Obviously, there is no counterpart to this kind of cryptanalytic attack in single-key systems.
Similarly, the RSA cryptoalgorithm (described in the section Cryptography: RSA encryption) is susceptible to a breakthrough in factoring techniques. In 1970 the world record in factoring was 39 digits. In 2009 the record was a 768-digit RSA challenge. That achievement explains why standards in 2011 called for moving beyond the standard 1,024-bit key (310 digits) to a 2,048-bit key (620 digits) in order to be confident of security through approximately 2030. In other words, the security of two-key cryptography depends on well-defined mathematical questions in a way that single-key cryptography generally does not; conversely, it equates cryptanalysis with mathematical research in an atypical way.

History of cryptology

There have been three well-defined phases in the history of cryptology. The first was the period of manual cryptography, starting with the origins of the subject in antiquity and continuing through World War I. Throughout this phase cryptography was limited by the complexity of what a code clerk could reasonably do aided by simple mnemonic devices. As a result, ciphers were limited to at most a few pages in size, i.e., to only a few thousands of characters. General principles for both cryptography and cryptanalysis were known, but the security that could be achieved was always limited by what could be done manually. Most systems could be cryptanalyzed, therefore, given sufficient ciphertext and effort. One way to think of this phase is that any cryptography scheme devised during those two millennia could have equally well been used by the ancients if they had known of it.
The second phase, the mechanization of cryptography, began shortly after World War I and continues even today. The applicable technology involved either telephone and telegraph communications (employing punched paper tape, telephone switches, and relays) or calculating machines such as the Brunsvigas, Marchants, Facits, and Friedens (employing gears, sprockets, ratchets, pawls, and cams). This resulted in the rotor machines used by all participants in World War II. These machines could realize far more complex operations than were feasible manually and, more importantly, they could encrypt and decrypt faster and with less chance of error. The secure size of ciphers grew accordingly, so that tens or even hundreds of thousands of characters were feasible. The switch from electromechanical devices to electronic ones accelerated this trend. To illustrate the progress that was made in only eight decades, in 1999 the U.S. government designed and fabricated a single silicon chip implementation of the Data Encryption Standard (DES) with a demonstrated throughput of 6.7 billion bits (6.7 gigabits) per second. The Advanced Encryption Standard (AES) can be implemented in a single silicon chip to handle 1010bits per second (10 gigabits per second) on an Internet backbone circuit. In a few seconds of operation, trillions of bits of cipher can be processed, compared with the tens of bits per second possible with the first mechanized cipher machines. By the end of the 20th century the volume of ciphertext that had to be dealt with on a single communications channel had increased nearly a billionfold, and it continues to increase at an ever-expanding rate.
The third phase, dating only to the last two decades of the 20th century, marked the most radical change of all—the dramatic extension of cryptology to the information age: digital signatures, authentication, shared or distributed capabilities to exercise cryptologic functions, and so on. It is tempting to equate this phase with the appearance of public-key cryptography, but that is too narrow a view. Cryptology’s third phase was the inevitable consequence of having to devise ways for electronic information to perform all of the functions that had historically been done with the aid of tangible documents.

Early cryptographic systems and applications

People have probably tried to conceal information in written form from the time that writingdeveloped. Examples survive in stone inscriptions, cuneiform tablets, and papyruses showing that the ancient Egyptians, Hebrews, Babylonians, and Assyrians all devised protocryptographic systems both to deny information to the uninitiated and to enhance its significance when it was revealed. The first recorded use of cryptography for correspondence was by the Spartans, who as early as 400 bc employed a cipher device called the scytale for secret communication between military commanders. The scytale consisted of a tapered baton, around which was spirally wrapped a strip of parchment or leather on which the message was then written. When unwrapped, the letters were scrambled in order and formed the cipher; however, when the strip was wrapped around another baton of identical proportions to the original, the plaintext reappeared. Thus, the Greeks were the inventors of the first transposition cipher. During the 4th century bc, Aeneas Tacticus wrote a work entitled On the Defense of Fortifications, one chapter of which was devoted to cryptography, making it the earliest treatise on the subject. Another Greek, Polybius (c. 200–118 bc), devised a means of encoding letters into pairs of symbols by a device called the Polybius checkerboard, which is a true biliteral substitution and presages many elements of later cryptographic systems. Similar examples of primitive substitution or transposition ciphers abound in the history of other civilizations. The Romans used monoalphabetic substitution with a simple cyclic displacement of the alphabet. Julius Caesaremployed a shift of three positions so that plaintext A was encrypted as D, while Augustus Caesarused a shift of one position so that plaintext A was enciphered as B. As many moviegoers noticed, HAL, the computer in 2001: A Space Odyssey (1968), encrypts to IBM using Augustus’s cipher.
The first people to understand clearly the principles of cryptography and to elucidate the beginnings of cryptanalysis were the Arabs. They devised and used both substitution and transposition ciphers and discovered the use of both letter frequency distributions and probable plaintext in cryptanalysis. As a result, by about 1412, al-Kalka-shandī could include a respectable, if elementary, treatment of several cryptographic systems in his encyclopaedia Ṣubīal-aīshī and give explicit instructions on how to cryptanalyze ciphertext using letter frequency counts complete with lengthy examples to illustrate the technique.
European cryptology dates from the Middle Ages, when it was developed by the Papal States and the Italian city-states. The first European manual on cryptography (c. 1379) was a compilation of ciphers by Gabriele de Lavinde of Parma, who served Pope Clement VII. This manual, now in the Vatican archives, contains a set of keys for 24 correspondents and embraces symbols for letters, nulls, and several two-character code equivalents for words and names. The first brief code vocabularies, called nomenclators, were gradually expanded and became the mainstay well into the 20th century for diplomatic communications of nearly all European governments. In 1470Leon Battista Alberti published Trattati in cifra (“Treatise on Ciphers”), in which he described the first cipher disk; he prescribed that the setting of the disk should be changed after enciphering three or four words, thus conceiving of the notion of polyalphabeticity. This same device was used almost five centuries later by the U.S. Army Signal Corps for tactical communications in World War I. (See figure.) Giambattista della Porta provided a modified form of a square encryption/decryption table and the earliest example of a digraphic cipher in De furtivis literarum notis (1563; “The Notorious Secret Literature”). The Traicté des chiffres (“Treatise on Ciphers”), published in 1586 by Blaise de Vigenère, contains the square encryption/decryption table bearing his name (see figure) and descriptions of the first plaintext and ciphertext autokey systems.
By the time of the American Civil War, diplomatic communications were generally secured using codes, and cipher systems had become a rarity for this application because of their perceived weakness and inefficiency. Cipher systems prevailed, however, for military tactical communications because of the difficulty of protecting codebooks from capture or compromise in the field. In the early history of the United States, codes were widely used, as were book ciphers. Book ciphers approximate onetime keys if the book used is lost or unknown. (A famous unsolved book cipher is the Beale cipher (c. 1820), which purports to give the location of a buried treasure in Bedford County, Virginia.) During the Civil War the Union Army made extensive use of transposition ciphers, in which a key word indicated the order in which columns of the array were to be read and in which the elements were either plaintext words or code word replacements for plaintext. The Confederate Army primarily used the Vigenère cipher and on occasion simple monoalphabetic substitution. While Union cryptanalysts solved most intercepted Confederate ciphers, the Confederacy in desperation sometimes published Union ciphers in newspapers, appealing for help from readers in cryptanalyzing them.

Developments during World Wars I and II

During the first two years of World War I, code systems were used for high-command and diplomatic communications, just as they had been for centuries, and cipher systems were used almost exclusively for tactical communications. Field cipher systems such as the U.S. Signal Corps’s cipher disk mentioned above, lacked sophistication (and security), however. Nevertheless, by the end of the war some complicated cipher systems were used for high-level communications, the most famous of which was the German ADFGVX fractionation cipher, described in the section Cryptography: Product ciphers.
The communications needs of telegraphy and radio and the maturing of mechanical and electromechanical technology came together in the 1920s to bring about a major advance in cryptodevices: the development of rotor cipher machines. Although the concept of a rotor had been anticipated in the older mechanical cipher disks, American Edward H. Hebern recognized in about 1917 (and made the first patent claim) that by hardwiring a monoalphabetic substitution in the connections from contacts on one side of an electrical disk (rotor) to contacts on the other side and then cascading a collection of such rotors, polyalphabetic substitutions of almost arbitrary complexity could be realized. A set of these rotors is usually arranged in a stack called a basket; the rotation of each of the rotors in the stack causes the next one to rotate, much as the wheels in an odometer advance 1/10 of a revolution for every full revolution of its driving wheel. In operation, the rotors in the stack provide an electrical path from contact to contact through all of the rotors. In a straight-through rotor system, closing the key contact on a typewriter-like keyboard sends a current to one of the contacts on the end rotor. The current then passes through the maze of interconnections defined by the remaining rotors in the stack and their relative rotational positions to a point on the output end plate, where it is connected to either a printer or an indicator, thereby outputting the ciphertext letter equivalent to the input plaintext letter.
Until 2003, Hebern was generally recognized as the inventor of the rotor encryption machine. In that year, scholars published research showing that in 1915, two years before Hebern’s work, a rotor machine had been designed and built by two Dutch naval officers, Lieut. R.P.C. Spengler and Lieut. Theo van Hengel, a second prototype built by a Dutch mechanical engineer and wireless operator, Lieut. W.K. Maurits, and the devices tested by the Dutch navy in the East Indies under the direction of Rear Adm. F. Bauduin. The navy declined to proceed with the project, however, and the participants did not immediately pursue a patent. At the end of World War I, Spengler and van Hengel sought to patent their idea, but the navy resisted declassifying their work. Meanwhile, Hebern had filed a patent claim in 1917, which held up through the years, and gradually the Dutch inventors were forgotten.
Starting in 1921 and continuing through the next decade, Hebern constructed a series of steadily improving rotor machines that were evaluated by the U.S. Navy and undoubtedly led to the United States’ superior position in cryptology as compared to that of the Axis powers duringWorld War II. The 1920s were marked by a series of challenges by inventors of cipher machines to national cryptologic services and by one service to another, resulting in a steady improvement of both cryptomachines and techniques for the analysis of machine ciphers. At almost the same time that Hebern was developing the rotor cipher machine in the United States, European engineers, notably Hugo A. Koch of the Netherlands and Arthur Scherbius of Germany, independently discovered the rotor concept and designed machines that became the precursors of the best-known cipher machine in history, the German Enigma used in World War II. (Seefigure.)
Another type of rotor machine is much more like the Vernam encryption system (see Substitution ciphers, above). Such devices are pin-and-lug machines, and they typically consist of a collection of rotors having a prime number of labeled positions on each rotor. At each position a small pin can be set to an active or inactive position. In operation, all of the rotors advance one position at each step. Therefore, if the active pin settings are chosen appropriately, the machine will not recycle to its initial pin configuration until it has been advanced a number of steps equal to the product of the number of positions in each one of the rotors. The figure shows a machine of this type, the Hagelin M-209 (named for the Swedish engineer Boris Hagelin) was used extensively by the U.S. military for tactical field communications during World War II. In the M-209 the rotors have 26, 25, 23, 21, 19, and 17 positions, respectively, so that the key period length is 101,405,850. (It is interesting to note that this length key would be exhausted in 1/100 of a second on an Internet backbone circuit today.) The relationship of this machine to the Vernam encryption system is not only through the way in which a lengthy binary sequence of active pin settings in the rotors is achieved by forming the product of six much shorter ones, but also in the way a symbol of plaintext is encrypted using the resulting key stream. Just behind the rotors is a “squirrel cage” consisting of 27 bars on each of which is a pair of movable lugs. Either or both of the lugs can be set in a position to be engaged and moved to the left on each step by a diverter actuated by the presence of an active pin on the corresponding rotor. The result is an effective gear wheel in which the number of teeth is determined by both the active pin settings and the movable lug settings. The number of teeth set determines the cyclical shift between one direct alphabet (plaintext) ABC…and a reverse standard alphabet ZYX….Thus, if no tooth were present, A would encrypt to Z, B to Y, and so forth, while one tooth present would cause A to encrypt to Y, B to Z, etc. This is strictly a Vernam-type encryption—i.e., encryption by subtraction modulo 26 of the key symbol from the plaintext symbol. To decrypt, the ciphertext is processed with the same pin settings that were used to encrypt it but with the cyclical shift set to occur in the opposite direction.
In 1930 the Japanese Foreign Office put into service its first rotor machine, which was code-named Red by U.S. cryptanalysts. In 1935–36 the U.S. Army Signal Intelligence Service (SIS) team of cryptanalysts, led by William F. Friedman, succeeded in cryptanalyzing Red ciphers, drawing heavily on its previous experience in cryptanalyzing the machine ciphers produced by the Hebern rotor machines. In 1939 the Japanese introduced a new cipher machine, code-namedPurple by U.S. cryptanalysts, in which rotors were replaced by telephone stepping switches. Because the replacement of Red machines by Purple machines was gradual, providing an enormous number of cribs between the systems to aid cryptanalysts, and because the Japanese had taken a shortcut to avoid the key distribution problem by generating keys systematically, U.S. cryptanalysts were able not only to cryptanalyze the Purple ciphers but also eventually to anticipate keys several days in advance. Functionally equivalent analogs to the Purple cipher machines were constructed by Friedman and his SIS associates, as seen in the figure, and used throughout the war to decrypt Japanese ciphers. Apparently no Purple machine survived the war. Another Japanese cipher machine, code-named Jade, was essentially the same as the Purple (seefigure). It differed from the latter chiefly in that it typed Japanese kana characters directly.
The greatest triumphs in the history of cryptanalysis were the Polish and British solution of the German Enigma ciphers and of two teleprinter ciphers, whose output was code-named Ultra, and the American cryptanalysis of the Japanese Red, Orange, and Purple ciphers, code-named Magic. These developments played a major role in the Allies’ conduct of World War II. Of the two, the cryptanalysis of the Japanese ciphers is the more impressive, because it was a tour de force of cryptanalysis against ciphertext alone. In the case of the Enigma machines, the basic patents had been issued in the United States, commercial machines were widely available, and the rotor designs were known to Allied cryptanalysts from a German code clerk. Although such factors do not diminish the importance of the Ultra intercepts, they did make the cryptanalysis easier.

The impact of modern electronics

In the years immediately following World War II, the electronic technology developed in support of radar and the recently discovered digital computer was adapted to cryptomachines. The first such devices were little more than rotor machines in which rotors had been replaced by electronically realized substitutions. The advantage of these electronic machines was speed of operation; the disadvantages were the cryptanalytic weaknesses inherited from mechanical rotor machines and the principle of cyclically shifting simple substitutions for realizing more complex product substitutions. In fact, rotor machines and electronic machines coexisted into the 1970s and early ’80s. There is little information in the open literature about the electronic cipher machines used by the various national cryptologic services, so the most reliable indication of cryptographic developments in the period from the final generation of rotor machines—the KL-7 developed by the United States for the North Atlantic Treaty Organization (NATO)—to the appearance of DES and public-key systems in 1976 is to be found in commercial equipment. (The KL-7 was withdrawn from service in June 1983; in 1985 it was learned that the Walker family spy ring had turned over a KL-7 device and keying material to the Soviets.)
One class of electronic devices that function similar to rotors is the Fibonacci generator (also called the Koken generator after its inventor), named for the Fibonacci sequence of number theory. In the classical Fibonacci sequence 1, 1, 2, 3, 5, 8, 13…each successive term, beginning with 2, is the sum of the two terms to its left; i.e., Fi = Fi − 1 + Fi − 2. By loose analogy, any sequence in which each term is the sum of a collection of earlier terms in fixed (relative) locations is called a Fibonacci sequence.
In an n-stage Fibonacci generator the contents of an n-bit shift register are shifted right one position at each step—the bit at the extreme right being shifted out and lost—and the new left-hand bit is determined by the logical sum (1 + 1 = 1, 0 + 1 = 1 + 0 = 0 + 0 = 0; symbolized by ⊕) of bits occurring in prescribed locations in the shift register before the shift was made. For example, for n = 5 and xi = xi − 1 ⊕ xi − 4 ⊕ xi − 5 one obtains the 31-bit cycle0101110110001111100110100100001which is the maximal-length sequence realizable with a five-stage generator. The relevance of Fibonacci generators to cryptography is seen if the sequence is read five bits at a time by successively shifting one bit position to the left. This yields a scrambled ordering of the integers 1 through 31 that resembles the scrambled ordering produced by rotors.
The cryptographic problem is that the combining operation used to determine successive states in the sequence is linear and hence easily invertible, even though the sequence can be 2n − 1 bits in length before repeating. Another problem is how the key is to be used. The obvious choice—i.e., simply to use the key to determine the number of steps in the cycle from the plaintext n-tuple to the ciphertext n-tuple—is cryptographically insecure because a known plaintext cryptanalysis would quickly reveal the key. A frequently reinvented solution to this problem has been to use the number found in selected locations of one maximal-length feedback shift register, in which the key is used as the initial register fill, to control the number of steps from the plaintext n-tuple to the ciphertext n-tuple in the cycle of another linear feedback shift register. In schemes of this sort the key register is generally stepped forward to hide the key itself before any encryption of plaintext is carried out and then advanced sufficiently many steps between encryptions to ensure diffusion of the keying variables. To encrypt an n-bit block of plaintext, the text is loaded into the main shift register and the machine stepped through a specified number of steps, normally a multiple of the number of bits in the key, sufficient to diffuse the information in the plaintext and in the key over all positions in the resulting ciphertext. To decrypt the resulting ciphertext it is necessary to have an inverse combiner function or for the original encryption function to be involutory—i.e., the encryption and decryption functions are identical, so that encrypting the ciphertext restores the plaintext. It is not difficult to design the feedback logic to make an involutory machine. Pictorially, the machine has simply retraced its steps in the cycle(s). Linearity in the logic, though, is a powerful aid to the cryptanalyst, especially if a matched plaintext/ciphertext attack is possible.
With a slight modification, this approach constitutes the basis of several commercially available cryptographic devices that function in a manner quite similar to the pin-and-lug cipher machines previously described. One such cryptomachine has six maximal-length linear feedback shift registers in which the stepping is controlled by another shift register; the contents of the latter are used to address a (nonlinear) lookup table defined by keys supplied by the user.
To avoid the problems associated with linearity, cryptographers have devised a number of nonlinear feedback logics that possess such desirable properties as diffusion of information (to spread the effects of small changes in the text) and large-cycle structure (to prevent exhaustive search) but which are computationally infeasible to invert working backward from the output sequence to the initial state(s), even with very many pairs of matched plaintext/ciphertext. The nonlinear feedback logic, used to determine the next bit in the sequence, can be employed in much the same way as linear feedback logic. The complicating effect of the key on the ciphertext in nonlinear logic, however, greatly contributes to the difficulty faced by the cryptanalyst. Electronic cipher machines of this general type were widely used, both commercially and by national cryptologic services.
The significance of the above historical remarks is that they lead in a natural way to the most widely adopted and used cipher in the history of cryptography—the Data Encryption Standard (DES).

The Data Encryption Standard and the Advanced Encryption Standard

In 1973 the U.S. National Bureau of Standards (NBS; now the National Institute of Standards and Technology) issued a public request for proposals for a cryptoalgorithm to be considered for a new cryptographic standard. No viable submissions were received. A second request was issued in 1974, and International Business Machines (IBM) submitted the patented Lucifer algorithm that had been devised by one of the company’s researchers, Horst Feistel, a few years earlier. The Lucifer algorithm was evaluated in secret consultations between the NBS and the National Security Agency (NSA). After some modifications to the internal functions and a shortening of the key size from 112 bits to 56 bits, the full details of the algorithm that was to become the Data Encryption Standard (DES) were published in the Federal Register in 1975. Following almost two years of public evaluation and comment, the standard itself was adopted at the end of 1976 and published at the beginning of 1977. As a consequence of certification of the standard by the NBS and its commitment to evaluate and certify implementations, it was mandated that the DES be used in unclassified U.S. government applications for the protection of binary-coded data during transmission and storage in computer systems and networks and on a case-by-case basis for the protection of classified information.
The use of the DES algorithm was made mandatory for all financial transactions of the U.S. government involving electronic fund transfer, including those conducted by member banks of the Federal Reserve System. Subsequent adoption of the DES by standards organizations worldwide caused the DES to become a de facto international standard for business and commercial data security as well.
The DES is a product block cipher in which 16 iterations, or rounds, of substitution and transposition (permutation) process are cascaded. The block size is 64 bits. The key, which controls the transformation, also consists of 64 bits; however, only 56 of these can be chosen by the user and are actually key bits. The remaining eight are parity check bits and hence totally redundant. The figure is a functional schematic of the sequence of events that occurs in one round of the DES encryption (or decryption) transformation. At each intermediate stage of the transformation process, the cipher output from the preceding stage is partitioned into the 32 left-most bits, Li, and the 32 right-most bits, Ri. Ri is transposed to become the left-hand part of the next higher intermediate cipher, Li + 1. The right-hand half of the next cipher, Ri + 1, however, is a complex function, Li + f(Ri, Ki + 1), of a subset of the key bits, Ki + 1, and of the entire preceding intermediate cipher. The essential feature to the security of the DES is that f involves a very special nonlinear substitution—i.e., f(A) + f(B) ≠ f(A + B)—specified by the Bureau of Standards in tabulated functions known as S boxes. This process is repeated 16 times. This basic structure, in which at each iteration the cipher output from the preceding step is divided in half and the halves transposed with a complex function controlled by the key being performed on the right half and the result combined with the left half using the “exclusive-or” from logic (true or “1” only when exactly one of the cases is true) to form the new right half, is called a Feistel cipher and is widely used—and not just in the DES. One of the attractive things about Feistel ciphers—in addition to their security—is that if the key subsets are used in reverse order, repeating the “encryption” decrypts a ciphertext to recover the plaintext.
The security of the DES is no greater than its work factor—the brute-force effort required to search 256 keys. That is a search for a needle in a haystack of 72 quadrillion straws. In 1977 that was considered an impossible computational task. In 1999 a special-purpose DES search engine combined with 100,000 personal computers on the Internet to find a DES challenge key in 22 hours. An earlier challenge key was found by the distributed Internet computers in 39 days and by the special-purpose search engine alone in 3 days. For some time it has been apparent that the DES, though never broken in the usual cryptanalytic sense, was no longer secure. A way was devised that effectively gave the DES a 112-bit key—ironically, the key size of the Lucifer algorithm originally proposed by IBM in 1974. This is known as “triple DES” and involves using two normal DES keys. As proposed by Walter Tuchman of the Amperif Corporation, the encryption operation would be E1D2E1 while decryption would be D1E2D1. SinceEkDk = DkEk = I for all keys k, this triple encryption uses an inverse pair of operations. There are many ways to choose the three operations so that the resultant will be such a pair; Tuchman suggested this scheme since if the two keys are both the same, it becomes an ordinary single-key DES. Thus, equipment with triple DES could be interoperable with equipment that only implemented the older single DES. Banking standards have adopted this scheme for security.
It may seem that DES is very different from the cryptosystems that preceded it—except that it is a product cipher made up of transpositions and substitutions—but it is in fact a logical continuation of them. In a sense the DES was the logical culmination of a long history of development of single-key cryptographic algorithms, and it is this aspect that has been emphasized in the discussion thus far. In another sense, however, the DES is quite different from anything that preceded it. Cryptology has traditionally been a secretive science, so much so that it was only at the end of the 20th century that the principles on which the cryptanalysis of the Japanese and German cipher machines of World War II were based were declassified and released. What is different about the DES is that it is a totally public cryptographic algorithm. Every detail of its operations—enough to permit anyone who wishes to program it on a microcomputer—is widely available in published form and on the Internet. The paradoxical result is that what is generally conceded to have been one of the best cryptographic systems in the history of cryptology was also the least secret.
In January 1997 the National Institute of Standards and Technology (NIST) issued a public request to submit candidates to replace the aging DES. This time 15 viable submissions from 12 countries were received. In October 2000 NIST announced that Rijndael, a program created by two Belgian cryptographers, Joan Daemen and Vincent Rijmen, had been accepted as the new standard, or the Advanced Encryption Standard (AES). The NBS had expected the DES to be implemented in special-purpose hardware and hence had given little or no consideration to its efficient implementation in software, i.e., using general-purpose microprocessors. As a result, the DES was unable to take advantage of the rapid development in microprocessors that occurred in the last two decades of the 20th century. The AES specifications, on the other hand, emphasized hardware and software implementations equally. In part, this recognized the needs of smart cards and other point-of-sale equipment, which typically have very limited computational capabilities, but more important was a recognition of the growing needs of the Internet and e-commerce. Based on their experience with the DES, where improvements in computing simply overran the work factor of the fixed 56-bit key, NIST specifications for the AES also called for the algorithm to be capable of increasing the key length if necessary. Rijndael proved itself to be both small enough to be implemented on smart cards (at less than 10,000 bytes of code) and flexible enough to allow longer key lengths.
Based on the DES experience, there is every reason to believe the AES will not succumb to cryptanalysis, nor will it be overrun by developments in computing, as was the DES, since its work factor can easily be adjusted to outpace them.
Gustavus J. SimmonsImages: Media for cryptologyVigenère cipher: substitution ciphersVigenère cipher: letter frequency analysisADFGVX ciphercipher diskEnigma: four-rotor modelHagelin M-209Purple cipher machineJade cipher machinecryptology: Data Encryption Standard operationTYPEX

Posted on  by  

A Brief History of Cryptography













Cryptology is a young science. Though it has been used for thousands of years to hide secret messages, systematic study of cryptology as a science (and perhaps an art) just started around one hundred years ago.
The first known evidence of the use of cryptography (in some form) was found in an inscription carved around 1900 BC, in the main chamber of the tomb of the nobleman Khnumhotep II, in Egypt. The scribe used some unusual hieroglyphic symbols here and there in place of more ordinary ones. The purpose was not to hide the message but perhaps to change its form in a way which would make it appear dignified. Though the inscription was not a form of secret writing, but incorporated some sort of transformation of the original text, and is the oldest known text to do so. Evidence of some use of cryptography has been seen in most major early civilizations. “Arthshashtra”, a classic work on statecraft written by Kautalya, describes the espionage service in India and mentions giving assignments to spies in “secret writing” – sounds like an ancient version of James Bond?
Fast forwarding to around 100 BC, Julius Caesar was known to use a form of encryption to convey secret messages to his army generals posted in the war front. This substitution cipher, known as Caesar cipher, is perhaps the most mentioned historic cipher in academic literature. (A cipher is an algorithm used for encryption or decryption.) In a substitution cipher, each character of the plain text (plain text is the message which has to be encrypted) is substituted by another character to form the cipher text (cipher text is the encrypted message). The variant used by Caesar was a shift by 3 cipher. Each character was shifted by 3 places, so the character ‘A’ was replaced by ‘D’, ‘B’ was replaced by ‘E’, and so on. The characters would wrap around at the end, so ‘X’ would be replaced by ‘A’.
It is easy to see that such ciphers depend on the secrecy of the system and not on the encryption key. Once the system is known, these encrypted messages can easily be decrypted. In fact, substitution ciphers can be broken by using the frequency of letters in the language.
During the 16th century, Vigenere designed a cipher that was supposedly the first cipher which used an encryption key. In one of his ciphers, the encryption key was repeated multiple times spanning the entire message, and then the cipher text was produced by adding the message character with the key character modulo 26. (Modulo, or mod, is a mathematical expression in which you calculate the remainder of a division when one number is divided by another.) As with the Caesar cipher, Vigenere’s cipher can also easily be broken; however, Vigenere’s cipher brought the very idea of introducing encryption keys into the picture, though it was poorly executed. Comparing this to Caesar cipher, the secrecy of the message depends on the secrecy of the encryption key, rather than the secrecy of the system.
At the start of the 19th century when everything became electric, Hebern designed an electro-mechanical contraption which was called the Hebern rotor machine. It uses a single rotor, in which the secret key is embedded in a rotating disc. The key encoded a substitution table and each key press from the keyboard resulted in the output of cipher text. This also rotated the disc by one notch and a different table would then be used for the next plain text character. This was again broken by using letter frequencies.
The Engima machine was invented by German engineer Arthur Scherbius at the end of World War I, and was heavily used by the German forces during the Second World War. The Enigma machine used 3 or 4 or even more rotors. The rotors rotate at different rates as you type on the keyboard and output appropriate letters of cipher text. In this case the key was the initial setting of the rotors. The Enigma machine was eventually broken by British cryptographers at Bletchley Park.  The Enigma machine’s cipher was eventually broken by Poland and the technology was later transferred to the British cryptographers who designed a means for obtaining the daily key.
Up to the Second World War, most of the work on cryptography was for military purposes, usually used to hide secret military information. However, cryptography attracted commercial attention post-war, with businesses trying to secure their data from competitors.
In the early 1970’s, IBM realized that their customers were demanding some form of encryption, so they formed a “crypto group” headed by Horst-Feistel. They designed a cipher called Lucifer. In 1973, the Nation Bureau of Standards (now called NIST) in the US put out a request for proposals for a block cipher which would become a national standard. They had obviously realized that they were buying a lot of commercial products without any good crypto support. Lucifer was eventually accepted and was called DES or the Data Encryption Standard. In 1997, and in the following years, DES was broken by an exhaustive search attack. The main problem with DES was the small size of the encryption key. As computing power increased it became easy to brute force all different combinations of the key to obtain a possible plain text message.
In 1997, NIST again put out a request for proposal for a new block cipher. It received 50 submissions. In 2000, it accepted Rijndael, and christened it as AES or the Advanced Encryption Standard.
To conclude, history teaches us:
1. The secrecy of your message should always depend on the secrecy of the key, and not on the secrecy of the encryption system. (This is known as Kerckhoffs’s principle.)
2. Related to the above, always use ciphers which have been publicly reviewed and have been established as a standard. Using “secret crypto” is bad, because just like the Caesar cipher, once the system is known, all messages can be decrypted. For example, if your key is compromised, an attacker could access your messages; however, if the attacker can compromise the crypto system itself, they can obtain the plain text of every message (not just for a single person) encrypted by that system.

A Short History of Cryptography

Fred Cohen 1990, 1995 Mirror: http://web.itu.edu.tr/~orssi/dersler/cryptography/Chap2-1.pdf

Cryptography is one of the oldest fields of technical study we can find records of, going back at least 4,000 years. It is quite noteworthy that of all the cryptosystems developed in those 4,000 years of effort, only 3 systems in widespread serious use remain hard enough to break to be of real value. One of them takes too much space for most practical uses, another is too slow for most practical uses, and the third is widely believed to contain serious weaknesses.,,

Cryptography probably began in or around 2000 B.C. in Egypt, where hieroglyphics were used to decorate the tombs of deceased rulers and kings. These hieroglyphics told the story of the life of the king and proclaimed the great acts of his life. They were purposefully cryptic, but not apparently intended to hide the text. Rather, they seem to have been intended to make the text seem more regal and important. As time went by, these writings became more and more complicated, and eventually the people lost interest in deciphering them. The practice soon died out.
Cryptology was (and still is to some extent) enshrouded in a vail of mystique to most people. It was because of this that the public began to acquaint cryptography with the black arts. It was often thought to be concerned with communication with dark spirits, and developed a bad image because of it's mentors. Most early cryptographers were scientists, but the common people were often convinced that they were also followers of the devil.
The ancient Chinese used the ideographic nature of their language to hide the meaning of words. Messages were often transformed into ideographs for privacy, but no substantial use in early Chinese military conquests are apparent. Genghis Khan, for example, seems never to have used cryptography.
In India, secret writing was apparently more advanced, and the government used secret codes to communicate with a network of spies spread throughout the country. Early Indian ciphers consisted mostly of simple alphabetic substitutions often based on phonetics. Some of these were spoken or used as sign language. This is somewhat similar to "pig latin" (igpay atinlay) where the first consenant is placed at the end of the word and followed by the sound "ay".
The cryptographic history of Messopotamia was similar to that of Egypt, in that cuneiforms were used to encipher text. This technique was also used in Babylon and Asyria. In the Bible, a Hebrew ciphering method is used at times. In this method, the last letter of the alphabet is replaced by the first, and vice versa. This is called 'atbash'. For example, the following table gives a translation of this sort for English. The word "HELLO" becomes "SVOOL". Try to decrypt the word "WVXIBKG" and see what you get.
ABCDEFGHIJKLMNOPQRSTUVWXYZ
ZYXWVUTSRQPONMLKJIHGFEDCBA

Figure 2.1 - An ATBASH Cipher
In the famous Greek drama the 'Iliad', cryptography was used when Bellerophon was sent to the king with a secret tablet which told the king to have him put to death. The king tried to kill him by having him fight several mythical creatures, but he won every battle.
The Spartans used a system which consisted of a thin sheet of papyrus wrapped around a staff (now called a "staff cipher"). Messages were written down the length of the staff, and the papyrus was unwrapped. In order to read the message, the papyrus had to be wrapped around a staff of equal diameter. Called the 'skytale' cipher, this was used in the 5th century B.C. to send secret messages between greek warriors. Without the right staff, it would be difficult to decode the message using the techniques available at that time. The following version of the alphabet demonstrates the technique. First we see the wrapped version of the alphabet, then the unwrapped version.
            ADGJMPSVY
            BEHKNQTWZ
            CFILORUX

        ADGJMPSVYBEHKNQTWZCFILORUX

Figure 2.2 - A Skytale Cypher
Another Greek method was developed by Polybius (now called the "Polybius Square"). The letters of the alphabet would be laid out in a five by five square (similar to the later Playfair method) with i and j occupying the same square. Rows and columns are numbered 1 to 5 so that each letter has a corresponding (row,column) pair. These pairs could easily be signaled by torches or hand signals. Decryption consists of mapping the digit pairs back into their corresponding characters. This system was the first to reduce the size of the symbol set, and in a loose sense it might be considered the forerunner of modern binary representations of characters. Try decoding the message on the right.
        \ 1 2 3 4 5
         \_________
        1|A B C D E        T=54
        2|F G H I J        H=32    5344 44 4435
        3|K L M N O        I=42    4224 24 3211
        4|P Q R S T        S=44
        5|U V W X Y/Z

Figure 2.3 - The Polybius Square (slightly modified)
Julius Ceasar used a system of cryptography (i.e. the 'Caesar Cipher') which shifted each letter 2 places further through the alphabet (e.g. Y shifts to A, R shifts to T, etc.). This is probably the first cipher used by most school children. In figure 2.4, the first row is plaintext, while the second row is the equivalent ciphertext. The distance of the displacement is not important to the scheme, and in fact, neither is the lexical ordering chosen. The general case of this sort of cipher is the "monoalphabetic substitution cipher" wherein each letter is mapped into another letter in a one to one fashion. Try decoding VJKU.
ABCDEFGHIJKLMNOPQRSTUVWXYZ
CDEFGHIJKLMNOPQRSTUVWXYZAB

Figure 2.4 - The Caesar Cypher
Cryptanalysis is the practice of changing ciphertext into plaintext without complete knowledge of the cipher. The Arabs were the first to make significant advances in cryptanalysis. An Arabic author, Qalqashandi, wrote down a technique for solving ciphers which is still used today. The technique is to write down all the ciphertext letters and count the frequency of each symbol. Using the average frequency of each letter of the language, the plaintext can be written out. This technique is powerful enough to cryptanalyze ANY monoalphabetic substitution cipher if enough cyphertext is provided.
During the Middle Ages, cryptography started to progress. All of the Western European governments used cryptography in one form or another, and codes started to become more popular. Ciphers were commonly used to keep in touch with ambassadors. The first major advances in cryptography were made in Italy. Venice created an elaborate organization in 1452 with the sole purpose of dealing with cryptography. They had three cipher secretaries who solved and created ciphers that were used by the government.
Leon Battista Alberti is was known as "The Father of Western Cryptology" in part because of his development of polyalphabetic substitution. Polyalphabetic substitution is any technique which allows different ciphertext symbols to represent the same plaintext symbol. This makes it more difficult to interpret ciphertext using frequency analysis. In order to develop this technique, Alberti analyzed the methods for breaking ciphers, and devised a cipher which would try to render these techniques invalid. He designed two copper disks that fit into each other, each with the alphabet inscribed upon it. To start enciphering, a predetermined letter on the inner disk is lined up with any letter on the outer disk, which is written as the first character of the ciphertext. The disks are kept stationary, with each plaintext letter on the inner disk aligned with a ciphertext letter on the outer disk. After a few words of ciphertext, the disks are rotated so that the index letter on the inner disk is aligned with a new letter on the outer disk, and in this manner, the message is enciphered. By rotating the disk every few words, the cipher changed enough to limit the effectiveness of frequency analysis. Even though this technique in its stated form is very weak, the idea of rotating the disks and therefore changing the cipher many times within a message was a major breakthrough in cryptography.
The next major step was taken in 1518, by Trithemius, a German monk who had a deep interest in the occult. He wrote a series of six books called 'Polygraphia', and in the fifth book, devised a table that repeated the alphabet with each row a duplicate of the one above it, shifted over one letter. To encode a message, the first letter of the plaintext is enciphered with the first row of the table, the second letter with the second row, and so on. This produces a message where all available ciphers are used before being repeated. Figure 2.5 shows a changing key cipher of this sort. Notice that the assignment of code symbols to plaintext symbols changes at each time step (T1,T2,...). In this system, the key repeats every 26 letters of ciphertext.
        ABCDEFGHIJKLMNOPQRSTUVWXYZ Plaintext
        FGUQHXSZACNDMRTVWEJBLIKPYO T00
        OFGUQHXSZACNDMRTVWEJBLIKPY T01
        YOFGUQHXSZACNDMRTVWEJBLIKP T02
        PYOFGUQHXSZACNDMRTVWEJBLIK T03
            ...
        GUQHXSZACNDMRTVWEJBLIKPYOF T25

Figure 2.5 - A Changing Key Cipher
In 1553, Giovan Batista Belaso extended this technique by choosing a keyword that is written above the plaintext, in a letter to letter correspondence. The keyword is restarted at the beginning of each new plaintext word. The letter of the keyword above the letter of the plaintext is the first letter of the cipher line to be used. In other words, if the plaintext letter is 'b', and it's keyword letter is 'r', then the line of the Trithemius cipher beginning with 'r' is used to encipher the letter 'b'.
The most famous cryptographer of the 16th century was Blaise de Vigenere (1523-1596). In 1585, he wrote 'Tracte des Chiffres' in which he used a Trithemius table, but changed the way the key system worked. One of his techniques used the plaintext as it's own key. Another used the ciphertext. The manner in which these keys are used is known as key scheduling, and is an integral part of the "Data Encryption Standard" (DES) [DESDOC77] which we will discuss later.
In 1628, a Frenchman named Antoine Rossignol helped his army defeat the Huguenots by decoding a captured message. After this victory, he was called upon many times to solve ciphers for the French government. He used two lists to solve his ciphers: "one in which the plain elements were in alphabetical order and the code elements randomized, and one to facilitate decoding in which the code elements stood in alphabetical or numerical order while their plain equivalents were disarranged." When Rossignol died in 1682, his son, and later his grandson, continued his work. By this time, there were many cryptographers employed by the French government. Together, they formed the "Cabinet Noir" (the "Black Chamber").
By the 1700's, "Black Chambers" were common in Europe, one of the most renown being that in Vienna. It was called 'The Geheime Kabinets-Kanzlei' and was directed by Baron Ignaz de Koch between 1749 and 1763. This organization read through all the mail coming to foreign embassies, copied the letters, resealed them, and returned them to the post-office the same morning. The same office also handled all other political or military interceptions, and would sometimes read as many as 100 letters a day. The English Black Chamber was formed by John Wallis in 1701. Until that time, he had been solving ciphers for the government in a variety of unofficial positions. After his death in 1703, his grandson, William Blencowe, who was taught by his grandfather, took over his position and was granted the title of Decypherer. The English Black Chamber had a long history of victories in the cryptographic world.
In the colonies, there was no centralized cryptographic organization. Decryption was done predominantly by interested individuals and men of the cloth. In 1775, a letter intercepted from Dr. Benjamin Church was suspected to be a coded message to the British, yet the American revolutionaries could not decipher it. Their problem was solved by Elbridge Gerry, who later became the fifth Vice-President, and Elisha Porter. The message proved Church guilty of trying to inform the Tories, and he was later exiled. Benedict Arnold used a code wherein each correspondent has an exact copy of the same 'codebook'. Each word of plaintext is replaced by a number indicating its position in the book (e.g. 3.5.2, means page 3, line 5, word 2). Arnold's correspondent was caught and hung, so the codebook wasn't used very much. The revolutionaries also employed ciphers during the war. Samuel Woodhull and Robert Townsend supplied General George Washington with much information about British troop strength and movements in and around New York City. The code they used consisted of numbers which replaced plaintext words. This code was written by Major Benjamin Tallmadge. For further assurance, they also used invisible ink.
The father of American cryptology is James Lovell. He was loyal to the colonies, and solved many British ciphers, some which led to Revolutionary victories. In fact, one of the messages that he deciphered set the stage for the final victory of the war.
Former Vice-President Aaron Burr and his assistant General James Wilkinson were exploring the Southwest for possible colonization at the expense of Spain, and there was some confusion as to whether this colony would belong to the United States or Aaron Burr. Wilkinson was a Spanish agent, and changed one of Burr's encrypted letters home to make it appear as if Burr's intentions were to carve out his own country. This letter fell into the hands of President Thomas Jefferson. Burr was tried and acquitted, but his name was tainted forever.
The 'wheel cipher' was invented by Thomas Jefferson around 1795, and although he never did very much with it, a very similar system was still in use by the US navy only a few years ago. The wheel cipher consisted of a set of wheels, each with random orderings of the letters of the alphabet. The key to the system is the ordering in which the wheels are placed on an axle. The message is encoded by aligning the letters along the rotational axis of the axle such that the desired message is formed. Any other row of aligned letters can then be used as the ciphertext for transmission. The decryption requires the recipient to align the letters of the ciphertext along the rotational axis and find a set of aligned letters that makes linguistic sense as plaintext. This will be the message. There is a very small probability that there will be two sensible messages from the decryption process, but this can be checked simply by the originator. Without knowing the orderings of symbols on the wheels and the ordering of wheels on the axle, any plaintext of the appropriate length is possible, and thus the system is quite secure for one time use. Statistical attacks are feasible if the same wheels are used in the same order many times.
        GJTXUVWCHYIZKLNMARBFDOESQP W1
        IKMNQLPBYFCWEDXGZAJHURSTOV

 W2
        HJLIKNXWCGBDSRVUEOFYPAMQZT

 W3
                  ...
        BDFONGHJIKLSTVUWMYEPRQXZAC

 Wn

Figure 2.6 - A Wheel Cipher
In 1817, Colonel Decius Wadsworth developed a set of two disks, one inside the other, where the outer disk had the 26 letters of the alphabet, and the numbers 2-8, and the inner disk had only the 26 letters. The disks were geared together at a ratio of 26:33. To encipher a message, the inner disk is turned until the desired letter is at the top position, with the number of turn required for this result transmitted as ciphertext. Because of the gearing, a ciphertext substitution for a character will not repeat itself until all 33 characters for that plaintext letter have been used. Unfortunately, Wadsworth never got credit for his design, because Charles Wheatstone invented an almost identical machine a few years after Wadsworth, and got all the credit.
In 1844, the development of cryptography was dramatically altered by the invention of the telegraph. Communication with the telegraph was by no means secure, so ciphers were needed to transmit secret information. The public's interest in cryptography blossomed, and many individuals attempted to formulate their own cipher systems. The advent of the telegraph provided the first instance where a base commander could be in instant communication with his field commanders during battle. Thus, a field cipher was needed. At first, the military used a Vigenere cipher with a short repeating keyword, but in 1863, a solution was discovered by Friedrich W. Kasiski for all periodic polyalphabetic ciphers which up until this time were considered unbreakable, so the military had to search for a new cipher to replace the Vigenere.
The Black Chambers of Europe continued to operate and were successful in solving most American ciphers, but without a war underway, their usefulness was diminished, and by 1850 they were dissolved.
The 'Playfair' system was invented by Charles Wheatstone and Lyon Playfair in 1854, and was the first system that used pairs of symbols for encryption. The alphabet is laid out in a random 5 x 5 square, and the text is divided into adjacent pairs. The two letters of the pair are located, and a rectangle is formed with the two letters at opposite corners. The letters at the other two corners are the two letters of ciphertext. This is very simple to use, but is not extremely difficult to break. The real breakthrough in this system was the use of two letters at a time. The effect is to make the statistics of the language less pronounced, and therefore to increase the amount of work and the amount of ciphertext required to determine a solution. This system was still in limited use in world war 2, and was very effective against the Japanese.
    IKMNQ
    LPBYF PLAINTEXT =  PL AI NT EX TZ
    CWEDX       =              =
    GZAHU

 LPMGMOXEAS = LP MG MO XE AS
    RSTOV

Figure 2.7 - A Playfair System
In 1859, Pliny Earle Chase, developed what is known as the fractionating or tomographic cipher. A two digit number was assigned to each character of plaintext by means of a table. These numbers were written so that the first numbers formed a row on top of the second numbers. The bottom row was multiplied by nine, and the corresponding pairs are put back in the table to form the ciphertext.
Kasiski developed a cryptanalysis method in 1863 which broke almost every existing cipher of that time. The method was to find repetitions of strings of characters in the ciphertext. The distance between these repetitions is then used to find the length of the key. Since repetitions of identically ciphered identical plaintext occur at distances which are a multiple of the key length, finding greatest common divisors of repetition distances will lead to the key length. Once the key length (N) is known, we use statistics on every Nth character and the frequency of use implies which character it represents in that set of ciphertext symbols. These repetitions sometimes occur by pure chance, and it sometimes takes several tries to find the true length of the key using this method, but it is considerably more effective than previous techniques. This technique makes cryptanalysis of polyalphabetic substitution ciphers quite straight forward.
During the Civil War (1861-1865), ciphers were not very complex. Many techniques consisted merely of writing words in a different order and substituting code words for proper names and locations. Where the Union had centralized cipher control, the Confederacy tended to let field commanders decide their own forms of ciphers. The Vigenere system was widely used by field commanders, and sometimes led to the Union deciphering messages faster than their Confederate recipients. The Confederacy used three keywords for most of its messages during the War, "Manchester Bluff", "Complete Victory", and "Come Retribution". They were quickly discovered by three Union cryptanalysts Tinker, Chandler, and Bates, and messages encoded using them were regularly deciphered by the Union. The use of common words as keys to cryptosystems has caused many plaintext messages to be discovered. In fact, the use of common words for passwords is the most common entry point in modern computer system attacks.
In 1883, Auguste Kerckhoffs wrote 'La Cryptographie Militaire' in which he set forth six basic requirements of cryptography. We note that the easily remembered key is very amenable to attack, and that these rules, as all others, should be questioned before placing trust in them.
ciphertext should be unbreakable in practice
the cryptosystem should be convenient for the correspondents
the key should be easily remembered and changeable
the ciphertext should be transmissible by telegraph
the cipher apparatus should be easily portable
the cipher machine should be relatively easily to use
In the beginning of the 20th century, war was becoming likely in Europe. England spent a substantial effort improving its cryptanalytic capabilities so that when the war started, they were able to solve most enemy ciphers. The cryptanalysis group was called 'Room 40' because of its initial location in a particular building in London. Their greatest achievements were in solving German naval ciphers. These solutions were greatly simplified because the Germans often used political or nationalistic words as keys, changed keys at regular intervals, gave away intelligence indicators when keys were changed, etc.
Just as the telegraph changed cryptography in 1844, the radio changed cryptography in 1895. Now transmissions were open for anyone's inspection, and physical security was no longer possible. The French had many radio stations by WW1 and intercepted most German radio transmissions. The Germans used a double columnar transposition that they called 'Ubchi', which was easily broken by French cryptanalysts.
In 1917, the Americans formed the cryptographic organization MI-8. It's director was Herbert Osborne Yardley. They analyzed all types of secret messages, including secret inks, encryptions, and codes. They continued with much success during and after WW1, but in 1929, Herbert Hoover decided to close them down because he thought it was improper to "read others' mail". Yardley was hard pressed to find work during the depression, so to feed his family, he wrote a book describing the workings of MI-8. It was titled "The American Black Chamber", and became a best seller. Many criticized him for divulging secrets and glorifying his own actions during the War. Another American, William Frederick Friedman, worked with his wife, Elizebeth Smith, to become "the most famous husband-and-wife team in the history of cryptology". He developed new ways to solve Vigenere-like ciphers using a method of frequency counts and superimposition to determine the key and plaintext.
Up to 1917, transmissions sent over telegraph wires were encoded in Baudot code for use with teletypes. The American Telephone and Telegraph company was very concerned with how easily these could be read, so Gilbert S. Vernam developed a system which added together the plaintext electronic pulses with a key to produce ciphertext pulses. It was difficult to use at times, because keys were cumbersome. Vernam developed a machine to encipher messages, but the system was never widely used.
The use of cryptographic machines dramatically changed the nature of cryptography and cryptanalysis. Cryptography became intimately related to machine design, and security personnel became involved with the protection of these machines. The basic systems remained the same, but the method of encryption became reliable and electromechanical.
In 1929, Lester S. Hill published an article "Cryptography in an Algebraic Alphabet" in "The American Mathematical Monthly". Each plaintext letter was given a numerical value. He then used polynomial equations to encipher plaintext, with values over 25 reduced modulo 26. To simplify equations, Hill transformed them into matrices, which are more easily multiplied. This method eliminates almost all ciphertext repetitions, and is not broken with a normal frequency analysis attack. It has been found that if a cryptanalyst has two different ciphertexts from the same plaintext, and if they use different equations of the same type, the equations can be solved, and the system is thus broken. To counter charges that his system was too complicated for day to day use, Hill constructed a cipher machine for his system using a series of geared wheels connected together. One problem was that the machine could only handle a limited number of keys, and even with the machine, the system saw only limited use in the encipherment of government radio call signs. Hill's major contribution was the use of mathematics to design and analyze cryptosystems.
The next major advance in electromechanical cryptography was the invention of the rotor. The rotor is a thick disk with two faces, each with 26 brass contacts separated by insulating material. Each contact on the input (plaintext) face is connected by a wire to a random contact on the output (ciphertext) face. Each contact is assigned a letter. An electrical impulse applied to a contact on the input face will result in a different letter being output from the ciphertext face. The simple rotor thus implements a monoalphabetic substitution cipher. This rotor is set in a device which takes plaintext input from a typewriter keyboard and sends the corresponding electrical impulse into the plaintext face. The ciphertext is generated from the rotor and printed and/or transmitted.
The next step separates the rotor from previous systems. After each letter, the rotor is turned so that the entire alphabet is shifted one letter over. The rotor is thus a "progressive key polyalphabetic substitution cipher with a mixed alphabet and a period of 26". A second rotor is then added, which shifts it's position one spot when the first rotor has completed each rotation. Each electrical impulse is driven through both rotors so that it is encrypted twice. Since both rotors move, the alphabet now has a period of 676. As more rotors are added the period increases dramatically. With 3 rotors, the period is 17,576, with 4 it is 456,976, and with 5 it is 11,881,376. In order for a 5 rotor cipher to be broken with frequency analysis, the ciphertext must be extremely long.
The rotor system can be broken because, if a repetition is found in the first 26 letters, the cryptanalyst knows that only the first rotor has moved, and that the connections are changed only by that movement. Each successive set of 26 letters has this property, and using equations, the cryptanalyst can completely determine this rotor, hence eliminating one rotor from the whole problem. This can be repeated for each successive rotor as the previous rotor becomes known, with the additional advantage that the periods become longer, and thus they are guaranteed to have many repetitions. This is quite complex to do by hand. The first rotor machine was invented by Edward Hugh Hebern in 1918, and he instantly realized what a success it could be. He founded a company called Hebern Electric Code, which he promised would be a great financial success. The company died in a bitter struggle, the Government bought some of his machines, and he continued to produce them on his own, but never with great success.
During Prohibition, alcohol was transported into the country by illegal smugglers (i.e. rum runners) who used coded radio communication to control illegal traffic and help avoid Coast Guard patrols. In order to keep the Coast Guard in the dark, the smugglers used an intricate system of codes and ciphers. The Coast Guard hired Mrs. Elizebeth Smith Friedman to decipher these codes, and thus forced the rum runners to use more complex codes, and to change their keys more often. She succeeded in sending many rum runners to jail.
During WW2, the neutral country Sweden had one of the most effective cryptanalysis departments in the world. It was formed in 1936, and by the time the war started, employed 22 people. The department was divided into groups, each concerned with a specific language. The Swedes were very effective in interpreting the messages of all the warring nations. They were helped, however, by bungling cryptographers. Often the messages that were received were haphazardly enciphered, or even not enciphered at all. The Swedes even solved a German cipher that was implemented on a Siemens machine similar to a Baudot machine used to encipher wired messages.
During WW2, the Americans had great success at breaking Japanese codes, while the Japanese, unable to break US codes, assumed that their codes were also unbreakable. Cryptanalysis was used to thwart the Japanese attack on Midway, a decisive battle in the South Pacific. The US had been regularly reading Japanese codes before the attack on Pearl Harbor, and knew of the declaration of war that was presented to the President just after the attack on Pearl Harbor, several hours before the Japanese embassy in Washington had decoded it. German codes in WW2 were predominantly based on the 'Enigma' machine, which is an extension of the electromechanical rotor machine discussed above. A British cryptanalysis group, in conjunction with an escaped group of Polish cryptanalysts, first broke the Enigma early in WW2, and some of the first uses of computers were for decoding Enigma ciphers intercepted from the Germans. The fact that these codes were broken was of such extreme sensitivity, that advanced knowledge of bombing raids on England was not used to prepare for the raids. Instead, much credit was given to radar, and air raids were given very shortly before the bombers arrived.
In 1948, Shannon published "A Communications Theory of Secrecy Systems" [Shannon49] . Shannon was one of the first modern cryptographers to attribute advanced mathematical techniques to the science of ciphers. Although the use of frequency analysis for solving substitution ciphers was begun many years earlier, Shannon's analysis demonstrates several important features of the statistical nature of language that make the solution to nearly all previous ciphers very straight forward. Perhaps the most important result of Shannon's famous paper is the development of a measure of cryptographic strength called the 'unicity distance'.
The unicity distance is a number that indicates the quantity of ciphertext required in order to uniquely determine the plaintext of a message. It is a function of the length of the key used to encipher the message and the statistical nature of the plaintext language. Given enough time, it is guaranteed that any cipher can be broken given a length of ciphertext such that the unicity distance is 1. The unicity distance is computed as:

H(K)/(|M|-H(M))

where H(K) is the information content [Shannon48] of the key, H(M) is the information content per symbol of the message, and |M| is the information content per symbol of the message assuming that all symbols are equally likely. If K is chosen at random, H(K)=|K|, so for randomly chosen letters in English, H(K)=|K|=log2(26)=4.7 bits. For a 26 letter alphabet, |M|=4.7 bits. After a lot of statistical analysis of text, H(M) was imperically found to be 2.9 bits for English, and thus the unicity distance for English is 1 when |M| is (4.7/1.8)*|K|. In other words, any time the length of all messages sent under a particular key in English exceeds 2.6 times the length of that key, the key and plaintext can eventually be determined.Shannon noted that in a system with an infinite length random key, the unicity distance is infinite, and that for any alphabetic substitution cipher with a random key of length greater than or equal to the length of the message, plaintext cannot be derived from ciphertext alone. This type of cipher is called a "one-time-pad", because of the use of pads of paper to implement it in WW2 and before.
The story of cryptography would be at an end if it weren't for the practical problem that in order to send a secret message, an equal amount of secret key must first be sent. This problem is not severe in some cases, and it is apparently used in the hot line between Moscow and Washington [Kahn67] , but it is not the ultimate solution for many practical situations.
For most human (and computer) languages, a key of a given length can only be guaranteed safe for 2-3 times the length of the key. From this analysis, it appears that any system with a finite key is doomed to failure, but several issues remain to be resolved before all hope for finite key cryptography is abandoned. By looking at Shannon's equation, we may find ways out of our delema.
The first line of exploration is to reduce the redundancy of the language to extend the length of ciphertext required for solution. From Shannon's equation, we see that as the content of a message approaches its actual length, the divisor goes to 0, and thus the length of ciphertext required to determine the plaintext goes to infinity. Data compression techniques [Huffman52] may be practically used to remove 99.9% of the redundancy of plaintext with a reasonable degree of efficiency, and we can thus easily generate systems in which the unicity distance goes to |K|/|M|*0.001 which is 1 when |M|=1000*|K|. For a key of 64 bits in length, we could expect to safely encipher up to 64,000 bits of information, or about 8 pages of double spaced text before the system becomes theoretically breakable. We could easily replace a 64 bit key every 4 pages of text to make breaking the system nearly impossible, assuming we can store and distribute a sequence of truly random keys.
Shannon assures us that systems are breakable with sufficient ciphertext, but also introduces the concept of "workload", which embodies the difficulty in determining plaintext from ciphertext given the availability of enough ciphertext to theoretically break the system. An alternative to increasing unicity distance is the use of systems that tend to increase the workload required to determine solutions to cryptograms. Two important concepts due to Shannon's paper are the "diffusion" and "confusion" properties. These form the basis for many modern cryptosystems because they tend to increase the workload of cryptanalysis.
Diffusion is the dissipation of the statistical structure behind the language being transmitted. As an example, making a different symbol for each English word makes statistical occurance rates for many words difficult to detect in the short run. It also increases the quantity of data needed to decode messages because each word is treated as a symbol, and increases the difficulty of analysis once sufficient data is gathered because meaningful words are rarely repeated and the possible number of sentences with 'the', 'and', 'or', and other similar oft repeated words, is very large. Similarly, the random use of obscure synonyms for recurrent words tends to dissipate the ability to make statistical attacks against this system since it tends to equalize the chances of different words in the language occurring in the plaintext and thus tends to delay the statistical analysis of word occurance. Strange sentence structures have a similar effect on the cryptanalysis process.
Confusion is the obscuring of the relationship between the plaintext, the key, and the ciphertext. As an example, if any bit of the key has a 50% chance of affecting any bit of the ciphertext, statistical attacks on the key require solving a large number of simultaneous equations. In a simple XOR encoding, where each bit of plaintext is XORed with a single bit of key to give a single bit of ciphertext, each key bit only effects a single ciphertext bit. For addition in a modulus, each key bit and input bit potentially effect each output bit (although not with 50% probability in this case). Multiplication or exponentiation in a modulus tends to increase confusion to a higher degree than addition, and is the basis for many ciphers.
Extensions to Shannon's basic theories include the derivation of an "index of coincidence" that allows approximations of key length to be determined purely from statistical data [Knight78] , the development of semi-automated techniques for attacking cryptosystems, and the concept of using computational complexity for assessing the quality of cryptosystems [Diffie76] .

Cryptography Defined/Brief History

If you want to keep information secret, you have two possible strategies: hide the existence of the information, or make the information unintelligible. Cryptography is the art and science of keeping information secure from unintended audiences, of encrypting it. Conversely, cryptanalysis is the art and science of breaking encoded data. The branch of mathematics encompassing both cryptography and cryptanalysis is cryptology.
Modern cryptography uses sophisticated mathematical equations (algorithms) and secret keys to encrypt and decrypt data.
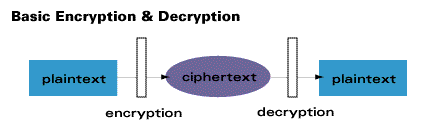
Encryption and Decryption
Today, cryptography is used to provide secrecy and integrity to our data, and both authentication and anonymity to our communications.

Modern Historical Overview

Cryptology was a public field in the United States until World War I, when the Army & Navy realized its value to national security and began working in secret. Through the early 1970s, cryptology was dominated by the government both because computers were very expensive and because the government released very little information. It returned to mainstream academic and scientific communities in a sort of cryptology renaissance when the computer revolution made computers more readily available and when demand for encryption increased due to fundamental changes in the ways America communicated.
The increase in demand for cryptography was driven by industry interest (e.g., financial services required secure electronic transactions and businesses needed to secure trade secrets stored on computers), and individual interest (e.g., secure wireless communications). Digital communications were obvious candidates for encryption.

Principles of Modern Cryptography

Modern cryptographers emphasize that security should not depend on the secrecy of the encryption method (or algorithm), only the secrecy of the keys. The secret keys must not be revealed when plaintext and ciphertext are compared, and no person should have knowledge of the key. Modern algorithms are based on mathematically difficult problems - for example, prime number factorization, discrete logarithms, etc. There is no mathematical proof that these problems are in fact are hard, just empirical evidence.
Modern cryptographic algorithms are too complex to be executed by humans. Today's algorithms are executed by computers or specialized hardware devices, and in most cases are implemented in computer software.
The design of secure systems using encryption techniques focuses mainly on the protection of (secret) keys. Keys can be protected either by encrypting them under other keys or by protecting them physically, while the algorithm used to encrypt the data is made public and subjected to intense scrutiny. When cryptographers hit on an effective method of encryption (a cipher), they can patent it as intellectual property and earn royalties when their method is used in commercial products. In the current open environment, many good cryptographic algorithms are available in major bookstores, libraries and on the Internet, or patent office.

Symmetric and Asymmetric Algorithms

There are two types of key-based encryption, symmetric (or secret-key) and asymmetric (or public-key) algorithms. Symmetric algorithms use the same key for encryption and decryption (or the decryption key is easily derived from the encryption key), while asymmetric algorithms use a different key for encryption and decryption, and the decryption key cannot be derived from the encryption key.
Symmetric algorithms can be divided into stream ciphers and block ciphers. Stream ciphers can encrypt a single bit of plaintext at a time, whereas block ciphers take a number of bits (typically 64 bits in modern ciphers), and encrypt them as a single unit. An example of a symmetric algorithm is DES.
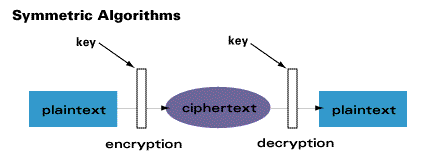
Symmetric Encryption with One Key
Asymmetric ciphers (also called public-key cryptography) make a public key universally available, while only one individual possesses the private key. When data is encrypted with the public key, it can only be decrypted with the private key, and vice versa. Public key cryptography adds a very significant benefit - it can serve to authenticate a source (e.g. a digital signature). Public key cryptography was invented by Whitfield Diffie and Martin Hellman in 1975. An example of an asymmetric algorithm is RSA.
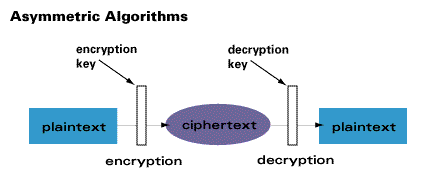
Asymmetric Encryption with Two Keys
In general, symmetric algorithms execute much faster than asymmetric ones. In real applications, they are often used together, with a public-key algorithm encrypting a randomly generated encryption key, while the random key encrypts the actual message using a symmetric algorithm. This combination is commonly referred to as a digital envelope.

Cryptography in Everyday Life

Authentication/Digital Signatures

Authentication and digital signatures are a very important application of public-key cryptography. For example, if you receive a message from me that I have encrypted with my private key and you are able to decrypt it using my public key, you should feel reasonably certain that the message did in fact come from me. If I think it necessary to keep the message secret, I may encrypt the message with my private key and then with your public key, that way only you can read the message, and you will know that the message came from me. The only requirement is that public keys are associated with their users by a trusted manner, for example a trusted directory. To address this weakness, the standards community has invented an object called a certificate. A certificate contains, the certificate issuer's name, the name of the subject for whom the certificate is being issued, the public key of the subject, and some time stamps. You know the public key is good, because the certificate issuer has a certificate too.
Pretty Good Privacy (PGP) is a software package originally developed by Phil Zimmerman that provides encryption and authentication for e-mail and file storage applications. Zimmerman developed his freeware program using existing encryption techniques, and made it available on multiple platforms. It provides message encryption, digital signatures, data compression, and e-mail compatibility. PGP uses RSA for key transport and IDEA for bulk encryption of messages. Zimmerman ran into legal problems with RSA over his use of the RSA algorithm in his program. PGP is now available in a couple of legal forms:MIT PGP versions 2.6 and later are legal freeware for non-commercial use, and Viacrypt PGP versions 2.7 and later are legal commercial versions of the same software.

Time Stamping

Time stamping is a technique that can certify that a certain electronic document or communication existed or was delivered at a certain time. Time stamping uses an encryption model called a blind signature scheme. Blind signature schemes allow the sender to get a message receipted by another party without revealing any information about the message to the other party.
Time stamping is very similar to sending a registered letter through the U.S. mail, but provides an additional level of proof. It can prove that a recipient received a specific document. Possible applications include patent applications, copyright archives, and contracts. Time stamping is a critical application that will help make the transition to electronic legal documents possible.

Electronic Money

The definition of electronic money (also called electronic cash or digital cash) is a term that is still evolving. It includes transactions carried out electronically with a net transfer of funds from one party to another, which may be either debit or credit and can be either anonymous or identified. There are both hardware and software implementations.
Anonymous applications do not reveal the identity of the customer and are based on blind signature schemes. (Digicash's Ecash) Identified spending schemes reveal the identity of the customer and are based on more general forms of signature schemes. Anonymous schemes are the electronic analog of cash, while identified schemes are the electronic analog of a debit or credit card. There are also some hybrid approaches where payments can be anonymous with respect to the merchant but not the bank (CyberCash credit card transactions) ; or anonymous to everyone, but traceable (a sequence of purchases can be related, but not linked directly to the spender's identity).
Encryption is used in electronic money schemes to protect conventional transaction data like account numbers and transaction amounts, digital signatures can replace handwritten signatures or a credit-card authorizations, and public-key encryption can provide confidentiality. There are several systems that cover this range of applications, from transactions mimicking conventional paper transactions with values of several dollars and up, to various micropayment schemes that batch extremely low cost transactions into amounts that will bear the overhead of encryption and clearing the bank.

Secure Network Communications

Secure Socket Layer (SSL)
Netscape has developed a public-key protocol called Secure Socket Layer (SSL) for providing data security layered between TCP/IP (the foundation of Internet-based communications) and application protocols (such as HTTP, Telnet, NNTP, or FTP). SSL supports data encryption, server authentication, message integrity, and client authentication for TCP/IP connections.
The SSL Handshake Protocol authenticates each end of the connection (server and client), with the second or client authentication being optional. In phase 1, the client requests the server's certificate and its cipher preferences. When the client receives this information, it generates a master key and encrypts it with the server's public key, then sends the encrypted master key to the server. The server decrypts the master key with its private key, then authenticates itself to the client by returning a message encrypted with the master key. Following data is encrypted with keys derived from the master key. Phase 2, client authentication, is optional. The server challenges the client, and the client responds by returning the client's digital signature on the challenge with its public-key certificate.
SSL uses the RSA public-key cryptosystem for the authentication steps. After the exchange of keys, a number of different cryptosystems are used, including RC2, RC4, IDEA, DES and triple-DES.
Kerberos 
Kerberos is an authentication service developed by MIT which uses secret-key ciphers for encryption and authentication. Kerberos was designed to authenticate requests for network resources and does not authenticate authorship of documents.
In a Kerberos system, there is a site on the network, called the Kerberos server, to perform centralized key management and administrative functions. The server maintains a key database with the secret keys of all users, authenticates the identities of users, and distributes session keys to users and servers who need to authenticate one another. Kerberos depends on a trusted third party, the Kerberos server, and if the server were compromised, the integrity of the whole system would be lost. Kerberos is generally used within an administrative domain (for example across a companies closed network); across domains (e.g., the Internet), the more robust functions and properties of public-key systems are often preferred.

Anonymous Remailers

A remailer is a free service that strips off the header information from an electronic message and passes along only the content. It's important to note that the remailer may retain your identity, and rather than trusting the operator, many users may relay their message through several anonymous remailers before sending it to its intended recipient. That way only the first remailer has your identity, and from the end point, it's nearly impossible to retrace.
Here's a typical scenario - the sender intends to post a message to a news group via three remailers (remailer 1, remailer 2, remailer 3). He encrypts the message with the last remailer's (remailer 3's) public key. He sends the encrypted message to remailer 1, which strips away his identity, then forwards it to remailer 2, which forwards it to remailer 3. Remailer 3 decrypts the message and then posts it to the intended newsgroup.
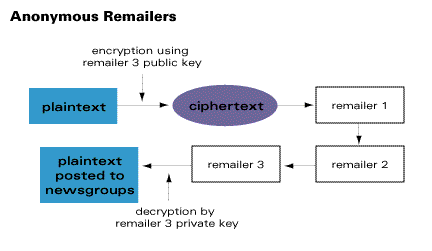
Anonymous Remailers

Disk Encryption

Disk encryption programs encrypt your entire hard disk so that you don't have to worry about leaving any traces of the unencrypted data on your disk.
PGP can also be used to encrypt files. In this case, PGP uses the user's private key along with a user-supplied password to encrypt the file using IDEA. The same password and key are used to unlock the file.

http://www.laits.utexas.edu/~anorman/BUS.FOR/course.mat/SSim/life.html


A Brief History of Cryptography

By Tony M. Damico
2009, VOL. 1 NO. 11 | (STUDENT PULSE, COMPUTER SCIENCE)
The earliest form of cryptography was the simple writing of a message, as most people could not read (New World, 2007). In fact, the very word cryptography comes from the Greek words kryptos and graphein, which mean hidden and writing, respectively (Pawlan, 1998).
Early cryptography was solely concerned with converting messages into unreadable groups of figures to protect the message’s content during the time the message was being carried from one place to another. In the modern era, cryptography has grown from basic message confidentiality to include some phases of message integrity checking, sender/receiver identity authentication, and digital signatures, among other things (New World, 2007).
The need to conceal messages has been with us since we moved out of caves, started living in groups and decided to take this civilization idea seriously. As soon as there were different groups or tribes, the idea that we had to work against each other surfaced and was proliferated, along with rankviolence, secrecy, and crowd manipulation. The earliest forms of cryptography were found in the cradle of civilization, which comes as no surprise, including the regions currently encompassed by Egypt, Greece and Rome.
As early as 1900 B.C., Egyptian scribes used hieroglyphs in a non-standard fashion, presumably to hide the meaning from those who did not know the meaning (Whitman, 2005). The Greek’s idea was to wrap a tape around a stick, and then write the message on the wound tape. When the tape was unwound, the writing would be meaningless. The receiver of the message would of course have a stick of the same diameter and use it to decipher the message. The Roman method of cryptography was known as the Caesar Shift Cipher. It utilized the idea of shifting letters by an agreed upon number (three was a common historical choice), and thus writing the message using the letter-shift. The receiving group would then shift the letters back by the same number and decipher the message (Taylor, 2002).
The Caesar Shift Cipher is an example of a Monoalphabetic Cipher. It is easy to see why this method of encryption is simple to break. All a person has to do is to go down the alphabet, juxtapositioning the start of the alphabet to each succeeding letter. At each iteration, the message is decrypted to see if it makes sense. When it does appear as a readable message, the code has been broken. Another way to break Monoalphabetic ciphers is by the use of what is known as frequency analysis, attributed to the Arabs circa 1000 C.E. (New World, 2007). This method utilizes the idea that certain letters, in English the letter "e," for instance, are repeated more often than others. Armed with this knowledge, a person could go over a message and look for the repeated use, or frequency of use, of a particular letter and try to substitute known frequently used letters (Taylor, 2002).
As for the Greek method of using a stick, once the method was known, it was a simple matter of trying out sticks of different diameters until the message became readable.
The art and science of cryptography showed no major changes or advancements until the Middle Ages. By that time, all of the western European governments were utilizing cryptography in one form or another. Keeping in touch with ambassadors was the major use of cryptography. One Leon Battista Alberti was known as “The Father of Western Cryptology,” most notably due to hisdevelopment of polyalphabetic substitution. His method was to use two copper disks that fit together. Each one of them had the alphabet inscribed on it. After every few words, the disks were rotated to change the encryption logic, thereby limiting the use of frequency analysis to crack the cipher (Cohen, 1990). Polyalphabetic substitution went through a variety of changes and is most notably attributed to Vigenere, although Rubin claims that he in fact had nothing to do with its creation. Rubin further points out that the use of the cipher disks continued in the Civil War, with the South using brass cipher disks, although the North regularly cracked the messages (2008).
Gilbert Vernam worked to improve the broken cipher, creating the Vernam-Vigenere cipher in 1918, but was unable to create one of significantly greater strength. His work did lead to the one time pad, which uses a key word only once, and it proved to be near unbreakable (Rubin, 2008). Whitman reports that criminals used cryptography during prohibition to communicate with each other.
Additionally, it is important to mention the recently popularized "windtalkers." The Navajo’s used their own language as a basis for cryptography (2005). The code was never broken and was instrumental in the victory in the Pacific Theatre during WWII. An argument could be made that the spoken language was not technically cryptography, but it should be noted that at every communication, the message was written down as a matter of procedure.
In modern times, the public key method of cryptography has seen wide adoption. The use of a common public key and a private key held only by the sender is in use today as a form of asymmetric encryption; one of the uses of this method is for the sender to use the private key to encrypt the message and then anyone who receives the message uses the public key to decipher it. In this way, the receiver knows who the message had to come from.
This method makes up the backbone of the Digital Signature. Problems arise when communications between multiple organizations require the use of many public keys and knowing when to use which one. No matter which method is used, a combination of methods applied one after the other will give the best result (Whitman, 2005).
In conclusion, it is somewhat surprising how limited the history of this very important topic is. No doubt cryptography and in a greater sense, cryptology, has played an enormous role in the shaping and development of many societies and cultures. While history may paint a different picture, the fact that the winners often write history is worth noting. If an army has a strong weapon that was instrumental in providing information that led to success, how apt are they to reveal it in the records of the wars? Instead, it may seem better to have idolized heroes  than to reveal the cloak and dagger methods that actually led to success. Crpytography, by its very nature, suggests secrecy and misdirection; therefore, the fact that the history of this topic is short and somewhat inaccessible is of no great surprise. Perhaps it is itself coded in what is has already been written.
Cohen, F (1990). A short history of cryptography. Retrieved May 4, 2009, from http://www.all.net/books/ip/Chap2-1.html New World Encyclopedia (2007).
Cryptography. Retrieved May 4, 2009, from http://www.newworldencyclopedia.org/entry/Cryptography
Pawlan, M. (1998, February). Cryptography: the ancient art of secret messages. Retrieved May 4, 2009, from http://www.pawlan.com/Monica/crypto/
Rubin, J. (2008). Vigenere Cipher. Retrieved May 4, 2009, from http://www.juliantrubin.com/encyclopedia/mathematics/vigenere_cipher.html
Taylor, K. (2002, July 31). Number theory 1. Retrieved May 4, 2009, from http://math.usask.ca/encryption/lessons/lesson00/page1.html
Whitman, M. & Mattord, H. (2005). Principles of information security. [University of Phoenix Custom Edition e-text]. Canada, Thomson Learning, Inc. Retrieved May 4, 2009, from University of Phoenix, rEsource, CMGT/432
Posted on 2013/08/14 by Huzaifa Sidhpurwala
↧
Search
Viewing all articles
Browse latest Browse all 11039

Trending Articles

Practice Sheet of Right form of verbs for HSC Students

September 22, 2019, 11:40 pm

Download: FK ft Shenky – Nakuyewa ”Prod by: Shenky”

February 16, 2017, 4:24 pm

How to win at Markstrat (Markstrat Tips and Tricks) – Vodites

January 5, 2014, 10:34 pm

Ominde Commission Report and Recommendations – Ominde Report of 1964

March 16, 2015, 5:14 am

Bureau of Internal Revenue: Regional Offices (Directory)

January 9, 2014, 11:06 pm

GO 53 on Enhancement of Ex-gratia upto 5 Lakhs Toddy Tappers in Telangana

March 26, 2017, 11:23 pm

Cakewalk CA-2A Leveling Amplifier v2.0.1.97 WiN, v2.0.1.96 OSX Incl Keygen

October 17, 2016, 7:20 am

Mp3 Download: Mdu - Kunjenjenjena

December 7, 2017, 8:16 am

How the kill the job , when DTP request running for long hours.

July 26, 2013, 2:41 am

Microsoft Intune から展開しているアプリのアップデートについて

October 17, 2016, 4:11 am

18-year-old girl was beaten for half an hour by two Northampton men in 'an...

September 1, 2017, 10:00 pm

Car crash in Dunton Bassett leaves driver in critical condition

October 7, 2014, 7:51 am

Macky 2, Two Others In Road Accident

March 29, 2015, 5:34 am

Application log 00000000000000089514: Could not convert queue DLVST90CLNT

May 14, 2015, 11:27 pm

Detroit mafia: D’Anna Brothers agree to plea deal

April 21, 2016, 6:56 am

Delivery block field greyed out using VA02

January 26, 2016, 2:52 pm

Muloraki Au

June 22, 2016, 1:44 am

【個人撮影】スマホのプライベート映像♪「中に出さないで///」カラオケ屋での生ハメ撮りが流出ｗ【リベンジポルノ】＠PornHub

October 12, 2017, 2:23 pm

BREAKING NEWS: Diamond Platnumz Is Reported Dead After Ghastly Car Accident

February 9, 2018, 4:56 am

FIAT 500 B0111 B0112

July 5, 2018, 10:31 am
Search
<script src="https://jsc.adskeeper.com/r/s/rssing.com.1596347.js" async> </script>