Rishi Atri Bhauma; devataa: Indra, Surya, Chanda: 1-3 us.n.ik, 5,9 anus.t.up, 4, 6-8 tris.t.up:
RV 5.40.5-6 refers to a solar eclipse:
यत् त्वा सूर्य स्वर्भानुस् तमसाविध्यद् आसुरः
अक्षेत्रविद् यथा मुग्धो भुवनान्य् अदीधयुः ||
स्वर्भानोर् अध यद् इन्द्र माया अवो दिवो वर्तमाना अवाहन्
गूळ्हं सूर्यम् तमसापव्रतेन तुरीयेण ब्रह्मणाविन्दद् अत्रिः ||
RV5.40.7-9:
मा माम् इमं तव सन्तम् अत्र इरस्या द्रुग्धो भियसा नि गारीत्
त्वम् मित्रो असि\सत्यराधास् तौ मेहावतम् वरुणश् च राजा
ग्राव्णो ब्रह्मा युयुजानः सपर्यन् कीरिणा देवान् नमसोपशिक्षन्
अत्रिः सूर्यस्य दिवि चक्षुर् आधात् स्वर्भानोर् अप माया अघुक्षत्
यं वै सूर्यम् स्वर्भानुस् तमसाविध्यद् आसुरः
अत्रयस् तम् अन्व् अविन्दन् नह्य् अन्ये अशक्नुवन् ||
Translation (based on Sayana):
When, Su_rya, the son of the Asura Svarbha_nu, overspread you with darkness, the worlds were beheld like one bewildered knowing not his place. [Svarbha_nu: is a name of ra_hu, the personified ascending node, the causer of an eclipse; he was a son of kas'yapa, by Danu, the mother of the Da_navas or asuras; another genealogy makes him the son of Vipraciti, by Sim.hika_, the sister of Hiran.yakas'ipu].
When, Indra, you were dissipating those illusions of Svarbha_nu which were spread below the sun, then Atri, by his fourth sacred prayer, discovered the sun concealed by the darkness impeding his functions. [i.e., by the four stanzas of this su_kta from the fifth to the eighth].
5.040.07 Su_rya speaks: Let not the violator, Atri, through hunger, swallow with fearful (darkness) me who am yours; you are Mitra, whose wealth is truth; do you and the royal Varun.a both protect me.
5.040.08 Then the Brahman, (Atri), applying the stones together, propitiating the gods with praise, and adoring them with reverence, placed the eye of Su_rya in the sky; he dispersed the delusions of Svarbha_nu.
5.040.09 The sun, whom the Asura, Svarbha_nu, had enveloped with darkness, the sons of Atri subsequently recovered; no others were able (to effect his release).
Sankhyayana Brahmana ( 24-4) expands this material further and gives us the total solar eclipse occurred three days before autumnal equinox.
Balakrishnan's conclusion on this eclipse date is 4677 BCE.
The latitude at which Atri made this observaton is identified close to 25 degree 12 min N.
Details follow, excerpted from his website.
Atri's Solar Eclipse
In the 5th Mandala of Rig Veda, the 40th sukta and 5th Rik, Rishi Atri describes a total solar eclipse.
Rig Veda- HYMN XL. 5.
Indra. Surya. Atri.

O Surya, when the Asura's descendant Svarbhanu, pierced thee through and through with darkness, All creatures looked like one who is bewildered, who knoweth not the place where he is standing.
Vedic astrology refers to moon’s ascending node or descending node at time of potential solar eclipse as Rahu or Swarbhanu, a demon. The passage certainly describes a total solar eclipse, magically imposed by Rahu, and people and animals being scared of the solar eclipse event .The same material is expanded in Kaushitiki or Sankhyayana Brahmana. 24.4.

In this segment reference is made to eclipse occurring three days before autumnal equinox. In Vedic times, equinoxes and solstices were well understood. Devayana (period of sun motion of gods) referred to time from spring equinox to autumnal equinox when sun stayed north of equator. Pitrayana(period of ancestral sun motion) referred to time from autumnal equinox to spring equinox when sun stayed south of equator. Gradually at later periods, but still historically at an old time, the Uttaraayana(Northerly motion of sun) from winter solstice to summer solstice and Dakshinayana (Southerly motion of sun) from summer solstice to winter solstice replaced the Devayana-Pitrayana use. Atri’s reference to Vishuvantam or autumnal equinox in context of Atri’s solar eclipse is significant and explicit. ThoughVishuvat stands for both equinoxes, the use in this context is taken to be autumnal because of beginning of Pitrayana.
Thus Atri’s RV 40-5 and Sankhyayana 24-4 provide us with details of a total solar eclipse occurring three days before autumnal equinox. Is this data unique enough to retro date the solar eclipse event and Atri’s time?
When European Indologists could translate and understand Rig Veda in late 1800’s Atri’s Solar eclipse and its astronomical implications caused a lot of excitement. Efforts were made to date the eclipse and hence Rig Veda. However, in those days without computers and precise mathematical models of sun-earth-moon motions currently available (in this present satellite era), retro dating of eclipses was difficult and results were ambiguous and unsuccessful. Dominance of Saros cycle approach resulted in too numerous solutions. B.G.Tilak, in his book Orion, describes the various efforts during his time.
Retro eclipse dating of eclipse events is a new approach to date historical events based on declared eclipses and their circumstances. Modern computer modeling of finely tuned heavenly body motion allow very precise calculation of the terrestrial eclipse times in ‘Universal Time’ frame. The only issue in retro dating is that there is a difference between ‘Universal Time’ and ‘Terrestrial Time’. Because of continuously changing difference, retro dating has some uncertainty. The earth’s rotation is inertial. Earths rotational momentum is always conserved, but the rotational speed varies with inertial distribution as mass on earth, which can slightly redistribute. This is similar to an ice skater changing spinning rate by inertia adjustment through hands. As the magma inside the earths core, ice ages, earthquake (like recent Indonesian Tsunami of 2005), all make miniscule changes earth’s inertia. This results in changes to earth’s rotational speed. Rotational speed change results in terrestrial time shifts relative to universal time. The time error is not large but can integrate to big numbers over thousands of years. This is called the delta T problem.
Retro eclipse dating of eclipse events is a new approach to date historical events based on declared eclipses and their circumstances. Modern computer modeling of finely tuned heavenly body motion allow very precise calculation of the terrestrial eclipse times in ‘Universal Time’ frame. The only issue in retro dating is that there is a difference between ‘Universal Time’ and ‘Terrestrial Time’. Because of continuously changing difference, retro dating has some uncertainty. The earth’s rotation is inertial. Earths rotational momentum is always conserved, but the rotational speed varies with inertial distribution as mass on earth, which can slightly redistribute. This is similar to an ice skater changing spinning rate by inertia adjustment through hands. As the magma inside the earths core, ice ages, earthquake (like recent Indonesian Tsunami of 2005), all make miniscule changes earth’s inertia. This results in changes to earth’s rotational speed. Rotational speed change results in terrestrial time shifts relative to universal time. The time error is not large but can integrate to big numbers over thousands of years. This is called the delta T problem.
Eclipse software
Mathematical models of heavenly bodies as seen from earth have always fascinated mankind who could find patterns in time. Examples of Mayan calendars, Indian, Chinese, Saros Cycle etc are examples.
Since Keplar’s time, mathematical modeling of the heavenly bodies in time and position has been of great interest to astronomers. Since the advent of computers the precision has increased many fold. Algorithms to provide positional and temporal data are well proven. Meeus’s work ‘Astronomical algorithms’ (ref) is a great example. Modern software for eclipses come in many forms, but generally use similar algorithms. The user interface and presentation of data may be different. Some examples are Planetary Software, Annala’s Lodestar pro, and Digital Universe by Syzygy Research & Technology etc.
DeltaT
Mathematical modeling of the earth’s delta T has been on going for some time and many models are available. The delta T is almost a full day of 86400 seconds by about 3000 BC. Many different models exist.. The International Astronomical Union in Rome adopted the following formula:
![]()
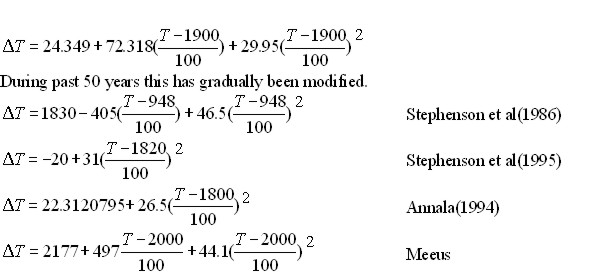
We overcome this problem in the context of Atri’s eclipse in a unique manner that will be presented in subsequent section.
The mathematical modeling of motions of earth and moon around sun has been perfected since Keplar’s initial work, and has reached a very high degree of accuracy particularly since the advent of space travel and computers. One such work by Jean Meeus [Ref-7] provides numerical algorithms, which take in to account many periodic terms in Moon motion including longitude, latitude, and distance from earth. Such algorithms are embedded in many software codes currently available on market. One such code is LodeStar Pro copy righted by Wayne C Annala in 1994 [Ref- 8]. Annala states that Lodestar pro results have been validated against databases from US Naval Observatory’s Interactive computer Ephemeris, and Jet Propulsion Laboratory in California. This article uses Annala’s Lodestar Pro for all eclipse estimations. Different researchers have addressed the issue of dating ancient and well-documented eclipses and arrived at appropriate DeltaT models. The table below lists results these historical eclipse studies. In order to develop confidence in Lodestar Pro used in this present study, following eclipses were checked with some changes to delta T appropriately.
| Date | Name | Eclipse | Ref | Location | Lodestar |
| 30 Nov 3340 BC | Irish Megalith | Solar | Griffin | Ireland | Yes |
| 09 August 2133BC | China Hsi/Ho | Solar | China | Yes | |
| 03 May 1375 BC | Ugarit Eclipse | Solar | Espenak | Yes | |
| 05 June 1302 BC | Early Chinese | Solar | Espenak | China | Yes |
| 16 April 1178 BC | Homer’s Odyssey | Solar | Espenak | North Africa | Yes |
| 20 April 899 BC | China-Double dawn | Solar | Espenak | China | Yes |
| 15 June 763 BC | Assyrian Eclipse | Solar | Espenak | Mesopotamia | Yes |
| 6 April 648 BC | Archilocus eclipse | Solar | Espenak | Yes | |
| 28 May 585 BC | Herodotus Thales Medes vs Lydians | Solar | Espenak | Yes | |
| 19 May 557 BC | Siege of Larisa | Solar | Espenak | Yes | |
| 02 Oct 480 BC | Xerxes’s eclipse | Solar | Espenak | Yes | |
| 03 Aug 431 BC | Peloponnesian war | Solar | Espenak | Yes | |
| 21 March 424 BC | Peloponnesian war –8th yr | Solar | Espenak | Yes |
Lodestar Pro could predict all these eclipses and approximate times for given locations suggesting that the algorithms used internally are in approximate agreement with other contemporary research data from others provided proper Delta T was used.
Resolving Delta T issue in context of Atri’s eclipse |
All eclipse search software need the following to identify locally visible eclipse
1) Longitude of observer
2) Latitude of Observer
3) Local time or time zone
4) Delta T
5) Period of search, from & to years and dates
Once this data is given, the software can identify the evolution and progress of the eclipse and provide all the relevant astronomical information.
1) Longitude of observer
2) Latitude of Observer
3) Local time or time zone
4) Delta T
5) Period of search, from & to years and dates
Once this data is given, the software can identify the evolution and progress of the eclipse and provide all the relevant astronomical information.
In case of Atri’s eclipse search, we lock the latitude of observation at 25 deg 12 min N. Then with a fixed delta T, realized by fixing a year range of a few years. (This will be varied from 1000 BC to 5000 BC in a total search pattern). We seek solar eclipse at 80 deg 54’ E. If an eclipse exists and the sun is between 0.6 to 1.5 deg N, we note the particulars. Then we keep changing the longitude by 30 deg steps or smaller till we can identify the peak eclipse. This process is continued for the full 360 degrees. All the eclipses and their magnitude that occur in sun range of our interest, namely +1.21 deg, are tabulated. The search pattern is continued similarly for the whole period of 1000 BC to 5000 BC in small increments, each covering full 360 deg around the earth at 25N latitude.
Thus the range of delta T we consider covers all terrestrial locations at 25 N. If an acceptable total eclipse occurs at +1.2 deg sun , it could be Atri’s eclipse. For such a case the deltaT=software deltaT+(longitudinal shift from 80deg52’)/15*3600 seconds. Such a search pattern we would have accommodated all possible delta T’s that can possibly exist. This process would remove the uncertainty in delta T.
Thus the range of delta T we consider covers all terrestrial locations at 25 N. If an acceptable total eclipse occurs at +1.2 deg sun , it could be Atri’s eclipse. For such a case the deltaT=software deltaT+(longitudinal shift from 80deg52’)/15*3600 seconds. Such a search pattern we would have accommodated all possible delta T’s that can possibly exist. This process would remove the uncertainty in delta T.
We illustrate this method of rendering delta T irrelevant for latitude based eclipse events. The famous Irish Megalith solar eclipse, by Griffin, was recently confirmed as occurring on 3340 November 30 at Longitude 7.1325 W and latitude of 53.7441 N. One significant feature of this finding is that there are pictorial carvings of the eclipse view perfectly in line with observation angle of sun. This corroboration makes the delta T estimates used very realistic. The delta T chosen for this Irish megalith eclipse was 104610 sec.
Irish megalith eclipse computed at different longitudes & different deltaT’s @ 53.74 N
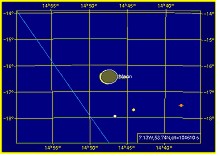 | 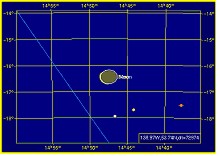 |
Paul Griffins Delta T @7W/53N | Annala’s Delta T @ 138W/53N |
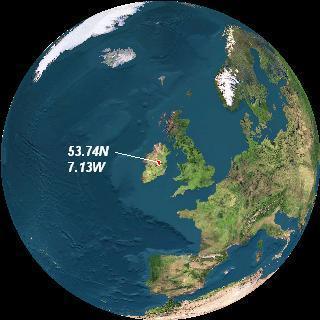 | 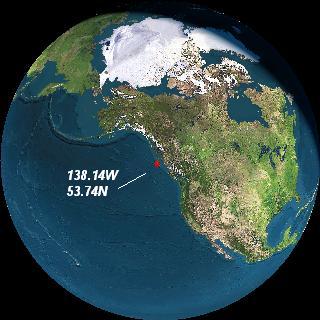 |
Eclipse location with deltaT=104610 sOver Ireland, 7W/53N | Eclipse location with deltaT=72974 s Over Pacific off coast US 138W/53N |
Wayne Annala’s Lodestar pro uses a delta T of 72974 seconds for 3340BC, nearly 31636s difference to Paul Griffin’s delta T, which correspond to 131 deg longitudinal shift in location. By keeping Annala’s delta T and a search of solar eclipse at all longitudes (latitude being same at 53.7441 N), we find that exact same eclipse would occur over pacific coast of North American continent at Longitude 131 deg away from Ireland. The angle difference is exactly corresponds to delta T difference*15/3600. Earth revolves 15 deg in 3600 seconds. This is illustrated above. Thus both the PC DOS Lodestar Pro and Apple based Digital Universe show same eclipse on same day and same time, if the delta T were same. Any difference in delta T shifts the location physically.
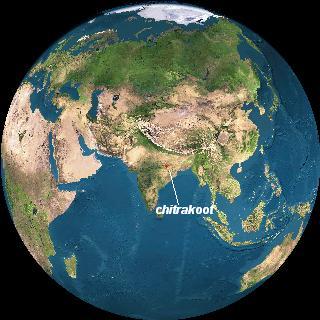
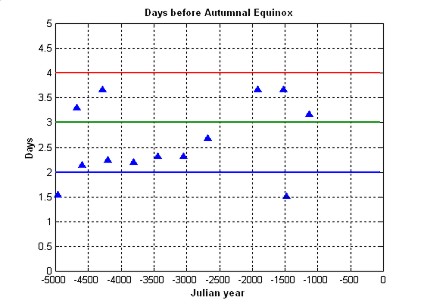
We assume that Atri’ Rishi lived at latitude of 25 deg N near Chitrakoot, in present day Uttar Pradesh and Madhya Pradesh province border in India. Location of Chitrakoot is shown in figure above. Association of Chitrakoot to Rishi Atri is made, based on local history of Chitrakoot, and reference to Atri in epic Ramayana by Valmiki. Further we assume that the ability of the people to identify Autumnal equinox was good and the error of estimate would be no more than half a day. We restrict our search of the solar eclipse to period older than 1000 BC, since no scholar has ever put the Vedas later than 1000 BC. We have made a search of all solar eclipses of sizable magnitude at latitude of 25 deg N and all longitudes of the earth covering 360 degrees, when sun was between 2 to 4 days from the autumnal equinox. A total of 13 eclipses have been found during the time period 1000 BC to 5000 BC, that occur about 2-4 days before autumnal equinox at a latitude of 25 deg N
| Julian Year | Annala deltaT,sec | Longitude @Maximum eclipse | Sun- deg @Maximum eclipse | Percentile eclipse | Corrected deltaT, sec to be seen at Chitrakoot |
| -1131September 30 | 22760 | 30d 54`E | +1.3 | 100% | 34760 |
| -1476 October 04 | 28431 | 37d 54E | +0.63 | 100% | 38751 |
| -1522 October 03 | 29235 | 129d 54E | +1.5 | 100% | 17514 |
| -1913 October 05 | 36520 | 95d 00E | +1.5 | 70% | 43620 |
| -2676 October 11 | 53071 | 44d 54W | +1.1 | 88% | 82831 |
| -3048 October 14 | 62250 | 100d 54E | +0.95 | 85% | 57450 |
| -3439 October 17 | 71500 | 85d 54E | +0.95 | 100% | 71500 |
| -3811 October 20 | 83390 | 68d 54E | +0.9 | 78% | 119395 |
| -4202 October 22 | 95427 | 34d 54E | +0.82 | 100% | 84627 |
| -4286 October 21 | 95998 | 161d00W | +1.5 | 88% | 153600 |
| -4593 October 23 | 100266 | 02d 00 W | +0.88 | 88% | 119360 |
| -4677 October 23 | 111130 | 115d 00W | +1.35 | 100% | 161430 |
| -4965 October 26 | 121233 | 148d 54E | +0.6 | 79% | 193233 |
Note that the equinox day is shifting continuously because of Earths precession over the period of 4000 years
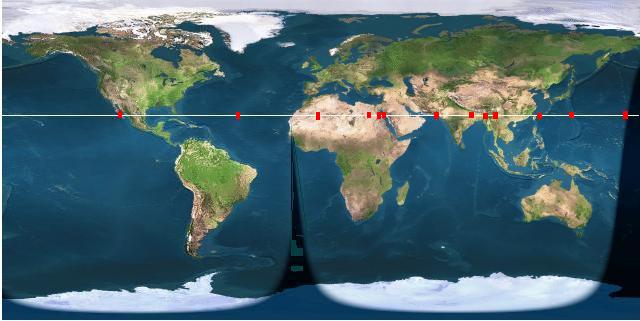
The figure shows location of all solar eclipses (@25 N latitude), which occur about 3 days before autumnal equinox all around the world (during 1000BC to 5000BC) using Annala’s Delta T model. By accounting for angular difference between apparent eclipse location and Chitrakoot, we can adjust the delta T so that all eclipses occur at Chitrakoot. The plot below shows the delta T required for eclipses to occur at Chitrakoot, and superimposes the same on various delta T models currently in literature. It also shows Irish megalith eclipse, and some ‘Historical eclipses’ by Espenak.
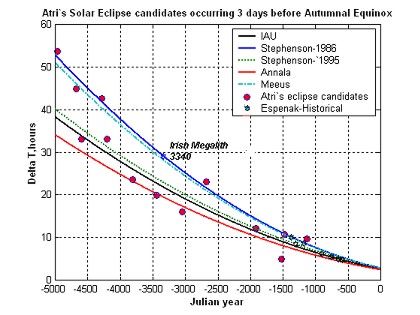
Discussion
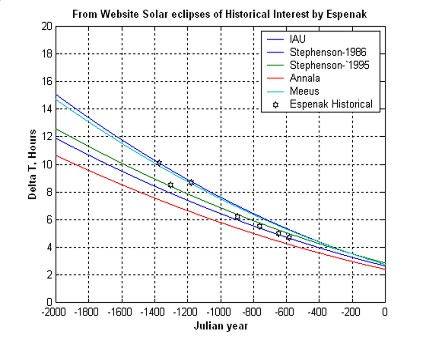
We have identified all solar eclipses that have occurred three days before autumnal equinox somewhere on earth at the latitude of 25 degrees. Any one of these thirteen can be Atri’s eclipse because of uncertainties in earth’s position or Delta T. To narrow the choice further, we need to decide on what the true deltaT would be corresponding to period concerned. It would appear that Knowledge of Delta T is still evolving, with many contemporary models proposed. A study of the Delta T used by Espenak (Ref 5) reveals scatter in Delta T he has used for his eclipses. His delta T’s are plotted as function of Julian year. It shows that some follow Meeus’s model and some Stephenson’s model. Some switch between the two. One would expect delta T being an integral function to be monotonic and smooth always slowing down. But two of his data shows speeding of earth. Thus modeling of Delta T is still not perfected to the degree of extreme confidence.
We now look at Atri’s solar eclipse candidates, with delta T adjusted to occur at Chitrakoot. Only one amongst these is a serious candidate. Recent Irish megalith eclipse appears to provide some corroboration of an eclipse in form of stone carvings. Other historical eclipses do not have such corroboration. In further analysis, we accept Stephenson (1986) model and Meeus’s mode as representative models very near each other
Stephenson 1986 model based analysis:
If we accept Stephenson 1986 model, best Atri’s eclipse purely from Delta T point of view are six candidates viz., 1131BC, 1476 BC, 1522 BC, 2676 BC, 4286 BC and 4965 BC dates
If we were to impose Stephenson’s model plus 3-day autumnal equinox requirement, then the candidates drop to five candidates viz., 1131BC, 1522 BC, 2676 BC, 4286 BC and 4965 BC.
IF were to demand Stephenson’s Delta T model plus 3-day to Autumnal equinox plus 100% eclipse at maximum, then the list drops to two candidates viz., 1131BC and 1522 BC.
Meeus’s Delta T Model
There are only two candidates if we were to use Meeus’s delta T model. They are the 1476 BC eclipse and the 4677 BC eclipse.
However, when we impose condition that the eclipse be 100% and occur 3-days before equinox, then only one candidate viz., 4677 BC eclipse meets all requirements.
All Known Delta T models
If we were to only go by 3-day requirement, following ten viz., 1131BC, 1522 BC, 1913 BC, 2676 BC, 3048 BC, 3439 BC, 4202 BC, 4286 BC, 4593 BC and 4676 BC would qualify
However, if we were to only go by 3-day requirement plus 100% eclipse the following five eclipses viz., 1131BC, 1522 BC, 3439 BC, 4202 BC and 4647 BC would qualify.
References
1) B.G.Tilak
Orion
Cosco Publications, reprint 1984, original 1895
Orion
Cosco Publications, reprint 1984, original 1895
2) S.Balakrishna
Dating Mahabharata-Two eclipses in thirteen days
http://www.vedicastronomy.net
Dating Mahabharata-Two eclipses in thirteen days
http://www.vedicastronomy.net
3) S Balakrishna
Names of stars from period of Vedas
1998
http://www.vedicastronomy.net
Names of stars from period of Vedas
1998
http://www.vedicastronomy.net
4) David Frawley
Sages, Gods and Kings
Sages, Gods and Kings
6) Paul Griffin,
http://www.astronomy.ca/3340eclipse/
7) Meeus, Jean. Astronomical Algorithms. Richmond, Willmann-Bell, 1998 ISBN 0-943396-63-8
http://www.astronomy.ca/3340eclipse/
7) Meeus, Jean. Astronomical Algorithms. Richmond, Willmann-Bell, 1998 ISBN 0-943396-63-8
8) M Ramakrishna Bhat
Varahamihira’s Brihat Samhita,
Motilal Banarasidas Publications, 1981
9) John Walker
http://www.fourmilab.ch/earthview/credits.html
http://www.fourmilab.ch/earthview/credits.html
10) Wayne Mitchell
Ancient Astronomical Observations and Near Eastern Chronology
Journal of Ancient Chronology Forum, Volume3
Ancient Astronomical Observations and Near Eastern Chronology
Journal of Ancient Chronology Forum, Volume3
http://www.vedicastronomy.net/deltat_references.htm
See: http://nopr.niscair.res.in/bitstream/123456789/29523/1/IJTK%2013(4)%20716-724.pdf Indian Journal of Traditional Knowledge, Vol. 13(4), October 2014, pp. 716-724. Vedic mythology of solar eclipse and its scientific validation by S. Santosh Kumarf and R. Rengaiyan
See: http://www.tifr.res.in/~archaeo/papers/Others/Eclipses%20in%20Ancient%20India.pdf Eclipses in ancient India by Mayank N Vahia and BV Subbarayappa, in: Proceedings of the 4th symposium on History of Astronomy, NOAJ, Japan, January 13-14, 2011, ed. Mitsuru Soma and Kiyotaka Tanikawa.
See: http://cincinnatitemple.com/articles/IndianAstronomy.pdf A profile of Indian astronomy before the Siddhantic period by RN Iyengar, presented at the ISERVE conference at Hyderabad on 14 December 2007
See: https://www.scribd.com/doc/102837118/Chronology-of-Vedic-Rshis-BN-Narahari-Achar-Vedic-Venues-No-1-2012 Chronology of Vedic Rishis, by BN Narahari Achar, Vedic Venues, No. 1, 2012
See: http://nopr.niscair.res.in/bitstream/123456789/29523/1/IJTK%2013(4)%20716-724.pdf Indian Journal of Traditional Knowledge, Vol. 13(4), October 2014, pp. 716-724. Vedic mythology of solar eclipse and its scientific validation by S. Santosh Kumarf and R. Rengaiyan
See: http://www.tifr.res.in/~archaeo/papers/Others/Eclipses%20in%20Ancient%20India.pdf Eclipses in ancient India by Mayank N Vahia and BV Subbarayappa, in: Proceedings of the 4th symposium on History of Astronomy, NOAJ, Japan, January 13-14, 2011, ed. Mitsuru Soma and Kiyotaka Tanikawa.
See: http://cincinnatitemple.com/articles/IndianAstronomy.pdf A profile of Indian astronomy before the Siddhantic period by RN Iyengar, presented at the ISERVE conference at Hyderabad on 14 December 2007
Svarbhānu or Swarbhanu (literally "Splendour of Radiance")[1] is a Hindu Asura (demon) traditionally held responsible for solar eclipses in Vedic mythology. The name is also used as an attribute of the demon Rahu in Puranic mythology,[1] who is also connected to solar eclipses.
Mythology
Svarbhānu is described as an asura twice in the Family Books of the Rig Veda.[2] Svarbhānu is described to strike the Sun with darkness, overshadowing the sun with darkness.[3] Stella Kramrisch considers this act as Svarbhānu as a deity greater than the sun.[1] The Rig veda further narrates after this, the king of heaven - Indra struck down Svarbhānu and sage Atri found the hidden sun and replaced it in the sky.[2][4] Svarbhanu again appears in the black Yajurveda and the Brahmanas.[2] According to theBrahmanas, Svarbhānu with darkness pierced Āditya (the Sun), whom, however, the gods set free by means of svara (accents).[5]
An assistant of Shukra, the teacher of the asuras and god of the planet Venus, was Svarbhānu, who quaffed the amrita proffered by Mohini, thereby achieving immortality as two beings : his head as Rahu, his body's trunk as Ketu.[6][7]
According to the Mahabharata, Svarbhānu is described to incarnate as Ugrasena, though here, Svarbhānu denotes Rahu. The Sun god Surya is also described by the attribute the "enemy of Svarbhānu".[8][9] Svarbhānu is described to strike both the sun and moon with arrows, the celestial bodies are revived by Atri as in the Rigveda.[4]
According to the text Hari-vaṃśa,[10] Svarbhānu ushered Kalanemi through the galaxy. In a Purana, Svarbhānu is described as son of the goddess Siṃhikā ('Little Lioness').[11]
Notes
1: a b c Stella Kramrisch, Raymond Burnier (1976). The Hindu temple 2. Motilal Banarsidass Publ. pp. 325–6. ISBN 978-81-208-0224-7.
2 a b c Wash Edward Hale (1986). Ásura- in early Vedic religion. Motilal Banarsidass. pp. 63–6. ISBN 978-81-208-0061-8.
3 Mitchiner 1982, p. 258
4 a b Antonio Rigopoulos. Dattātreya: the immortal guru, yogin, and avatāra. pp. 3–4.
5 Jaiminīya Brāhmaṇa 2:386; Maitrāyaṇi Brāhmaṇa 4:5:2
6 Chander 2000, p. 2
7 B S Shylaja, H R Madhusudan (1999). Eclipse. Universities Press. p. 2. ISBN 978-81-7371-237-1.
8"Sambhava" parvan, Section LXVII
9 Johannes Adrianus Bernardus van Buitenen (1981). The Mahabharata 2. University of Chicago Press. pp. 242, 784. ISBN 978-0-226-84664-4.
10 1:47:52
11 Kāla-Sarpa Yoga
References
- J. Sarat Chander : "Ketu and its Forms". 2000.
- Sukumari Bhattacharji : The Indian Theogony. Cambridge University Press, 1970.
- John E. Mitchiner : Traditions of the Seven Rishis. Motilal Banarsidass, Delhi, 1982.
See: https://www.scribd.com/doc/102837118/Chronology-of-Vedic-Rshis-BN-Narahari-Achar-Vedic-Venues-No-1-2012 Chronology of Vedic Rishis, by BN Narahari Achar, Vedic Venues, No. 1, 2012