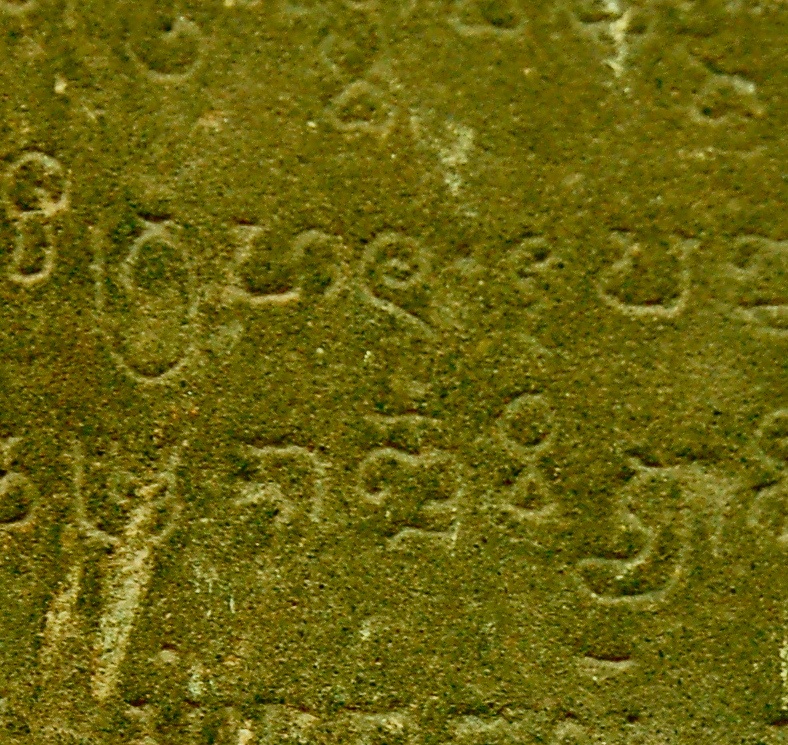Denoting śaka era 605

"Until 1930, many scholars in the West believed that the zero was either a European or an Arab invention. A highly polemical academic argument was raging at the time, where British scholars, among them G. R. Kaye, who published much about it, mounted strong attacks against the hypothesis that the zero was an Indian invention. The oldest known zero at that time was indeed in India, at the Chatur-bujha temple in the city of Gwalior. But it was dated to the mid-ninth century, an era that coincided with the Arab Caliphate. Thus Kaye's claim that zero was invented in the West and came to India through Arab traders could not be defeated using the Gwalior zero.

"But then in 1931, the French archaeologist Georges Cœdès published an article (see reference below) that demolished Kaye's theory. In it, he proved definitively that the zero was an Eastern (and perhaps Cambodian, although he viewed Cambodia an "Indianized" civilization) invention. Cœdès based his argument on an amazing discovery. Early in the twentieth century, an inscription was discovered on a stone slab in the ruins of a seventh-century temple in a place called Sambor on Mekong, in Cambodia. Cœdès gave this inscription the identifier K-127. He was an expert philologist and translated the inscription from Old Khmer. It begins:
Chaka parigraha 605 pankami roc...

"Translated: The Chaka era has reached 605 on the fifth day of the waning moon...

:The zero in the number 605 is the earliest zero we have ever found. We know that the Chaka era began in AD 78, so the year of this inscription in our calendar is 605 + 78 = AD 683. Since this time predates the Arab empire, as well as the Gwalior zero, by two centuries, Cœdès was able to prove that the zero is, in fact, an Eastern invention. It is believed to have come to the West via Arab traders and was popularized in Europe through the work of Fibonacci (of the famous sequence of numbers), published in 1202.

"For a time, inscription K-127 was kept in the Cambodian National Museum in Phnom Penh. But during the Khmer Rouge reign of terror, while killing more than 1.7 million of their own people, Pol Pot and his henchmen also stole or destroyed close to 10,000 artifacts -- and this priceless inscription's whereabouts were unknown."

http://www.khmer-network.com/forum/viewthread.php?tid=9760

Not the earliest zero, rediscovered

A rather unfortunate effort in Discover by Amir Aczel, ‘How I Rediscovered the Oldest Zero in History’ more or less effaces his solid legwork with shoddy theorizing and ahistorical claims.  Supported by the Sloan Foundation, Aczel (a popular science writer) went to Cambodia and tracked down the location of the Old Khmer inscription from Sambor, which is dated 605 in the Saka era (equivalent to 683 CE), which obviously contains a zero.    While the Hindu-Arabic-Western numerical tradition is seen to emanate from India, all of our earliest unquestioned examples (the late 7th century ones) of the zero are from Southeast Asia, and Sambor is the earliest one.  Because things have been rough in Cambodia for a long time, his work tracking it down and ensuring that it would be protected deserves a lot of credit.

If he had stopped there it would have been fine. Unfortunately, in an effort to bolster the importance of his claim, Aczel spends quite a lot of time justifying this as the first zero anywhere, ever, neglecting Babylonian and Maya zeroes from many centuries earlier.  To do that he needs to whip out all sorts of after-the-fact justifications of why those zeroes don’t really count, because Babylonians didn’t use their zero as a pure placeholder, or because Maya zeroes, well actually he just ignores those until the comments (but don’t read the comments – really, folks, that is the first rule of the internet).   Just for kicks, and regardless of the fact that it has nothing to do with zero, he starts off with a lengthy diatribe about how the Roman numerals are ‘clunky’ and ‘cumbersome’ and ‘inefficient’, which as long-time readers of this blog, or anyone who has read Numerical Notation, will know, is an utterly ridiculous, ahistorical claim that is divorced from how such numerals were actually used over two millennia.

I have come to terms with the fact that I will probably be spending the rest of my career pointing out that absolute judgements of the efficiency of numeral systems run the gamut from ‘missing the point’ to ‘completely ahistorical’ to ‘rabidly ethnocentric’.  While Aczel’s piece is not the worst of the sort, it certainly doesn’t deserve much praise.  Which is a shame, since that Sambor inscription really is the first known zero in the Indian tradition (to which our own Western numerals owe their origin) and it’s great that he’s been able to reconfirm its location in a politically perilous part of the world.

http://glossographia.wordpress.com/2013/06/02/not-the-earliest-zero-rediscovered/

How I Rediscovered the Oldest Zero in History

By Amir Aczel | May 20, 2013 1:31 pm

Mathematically, the Greco-Roman-Etruscan number system is an endlessly repetitive number system that is inefficient and cumbersome. To write 3333, which we do by repeating the sign 3 four times, a Roman would have had to scribble down MMMCCCXXXIII—three times as many characters. And I challenge anyone to multiply this number by MMDCCCLXXIX—usingonly the Roman system (meaning without translating these numbers into what they would be in our base-10 number system and then back into Roman numerals). Surprisingly, this clunky old Roman number system, with its ancient Greek and Etruscan roots, remained in use in Europe until the thirteenth century!

Our base-10 system derives its power and efficiency from the fact that we use a zero. The zero here is not just a concept of nothingness (and something every schoolchild learns you are forbidden to divide by), but also a place holder. The zero is a sign we place in a location in a number when there is nothing there—to tell us, for example, that 40 means four tens and no units, or that 405 is four hundreds, no tens, and five units.

Numbers on a dial

The zero thus turns the numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 into what algebraists call thering Z(10). When you stack such rings one on top of the other, and you let them represent, in turn, the units, tens, hundreds, thousands, ten thousands, and so on, based on each ring’s location, you get the highly efficient number system we have today. Think of each ring as a dial—when it goes around full circle, you get 0 and you add a 1 to the ring above it. As an example, start with the number 5—this means only the lowest ring, that of the units, is nonempty, and has the number 5. Now add to this the number 7. Five units from the 7 will bring the units ring to 0 and make the tens ring jump up to 1. The remaining 2 from the 7 will make the lowest ring (the lowest dial) now show 2. Thus we have that the sum of 5 and 7 is 12. Without the place-holding zero, which makes each “dial” start repeating itself after going through zero, we couldn’t do this.

The ancient Babylonians (preceded by the Akkadians and Sumerians) had a base-60 number system, without a zero. So already 4,000 years ago, people in ancient Babylon understood that it is efficient to make numbers become “circular” or dial-like, in the sense that 60 was like our 10, and 3600 (60 squared) was like our 100, and so on. But the Babylonians didn’t use a place-holding zero, so there were serious ambiguities in their system.

Our number system is far superior to the old Babylonian base-60 system, because our base is much smaller and because we use a zero, and it is also superior to the 3,000-year-old Greco-Roman-Etruscan letter-based system. Zero is the incredible invention that made our number system so efficient. This system was popularized in Europe after the publication, in 1202, of the book Liber Abaci (The Book of the Abacus), by Fibonacci (of the famous Fibonacci sequence). Presumably, Fibonacci learned the use of the 10 numerals with zero from Arab traders, with whom he dealt on behalf of his merchant father, and that is why we often call them the Arabic numerals. But Fibonacci himself refers to them in his book as the “nine Indian numerals” with zero, which he calls zephirum, perhaps originating from the Arab sefir.

The original zero

But who invented the zero, which gives so much power to our number system? We don’t know who invented it, but we are pretty sure that the zero is an Eastern invention. The oldest zero in India with a confirmed date is from the mid-ninth century, and found in the Chatur-bujha temple in the city of Gwalior.

At one point, an older zero was known. In the 1930s a zero from the year AD 683 was found in Cambodia, and its great antiquity allowed a French researcher by the name of Georges Coedes to prove that the zero is of Eastern provenance. This is because, while the Gwalior zero is concurrent with the Arab empire based in Baghdad (the Caliphate), the zero from 683 predates extensive Arab trading. It also comes from a location that is much farther east than India. Its existence thus makes it highly unlikely that the zero was invented in Europe or Arabia and traveled east through Arab traders, as some had believed in the early 20th century. The Cambodian zero proved that zero was an Eastern invention. But this zero disappeared during the Khmer Rouge regime in Cambodia, and no one knew if it still existed.

I felt very strongly that it was important to recover the world’s oldest zero. I spent five years researching its whereabouts and developed various hypotheses about where it might be found. Then last year I was awarded a generous research grant from the Alfred P. Sloan Foundationin New York, which enabled me to travel to Cambodia to search for this precious find. As is well known, Cambodian artifacts have been plundered for decades and sold illegally on the international antiquities markets. During the Khmer Rouge era, while killing 1.7 million of their own people, Pol Pot and his henchmen also looted, vandalized or destroyed more than 10,000 ancient statues or inscriptions.

The location where the oldest zero in the world—on a seventh-century stone inscription—was kept was plundered by the Khmer Rouge as late as 1990. I traveled to that location, not far from the famous Angkor Wat temple, and after weeks of searching among thousands of artifacts, many of them damaged or discarded, I was able to discover the inscription. It is shown in the photo below, taken by my wife.

Inscription K-127, from Sambor on Mekong. Photo Credit: Debra Gross Aczel

"Below is the only picture (with a few others my wife took) that exists of this priceless find. Cœdès had used only a pencil-rubbing, and never had a photograph. The dot in the center, to the right of the inverted-9-looking sign (which is 6 in Old Khmer) is the oldest zero ever discovered. His Excellency Hab Touch has promised me to bring K-127 back to the Cambodian National Museum in Phnom Penh, where it belongs, and where, hopefully, everyone would soon be able to see it."

Photo Credit: Debra Gross Aczel 

References:
Cœdès, Georges, "A propos de l'origine des chiffres arabes," Bulletin of the School of Oriental Studies, University of London, Vol. 6, No. 2, 1931, pp. 323-328. 
Diller, Anthony, "New Zeros and Old Khmer," The Mon-Khmer Studies Journal, Vol. 25, 1996, pp. 125-132. 

Ifrah, Georges. The Universal History of Numbers. New York: Wiley, 2000.

See: http://www.huffingtonpost.com/amir-aczel/worlds-first-zero_b_3276709.html

The zero is the dot in the middle, to the right of the spiral-looking character, which is a 6 in Old Khmer. The numeral to the right of the dot is a 5, making the full number 605. The inscription says: “The Chaka era reached year 605 on the fifth day of the waning moon…” We know that in Cambodia the Chaka era began in the year 78 AD. Thus the date of this zero is 605 + 78 = 683.

I notified the Cambodian Government of my discovery, and His Excellency Hab Touch of the Cambodian Ministry of Culture and Fine Arts, who had helped me in my search, promised me to place this inscription—one of the most important finds in the history of science—in the Cambodian National Museum in Phnom Penh, where it rightly belongs. So anyone interested in the history of science and the birth of numbers should soon be able to see the first zero ever discovered.

Amir D. Aczel writes often about physics and cosmology. His book about the discovery of the Higgs boson, Present at the Creation: Discovering the Higgs Boson, was published in paperback by Broadway Books in November 2012.

Top image by yanugkelid / Shutterstock

Leave a message...

• Best
• Community
• Share 

• nashv • 13 days ago

  You seem to have forgotten Aryabhatta, who while never used the symbol for zero because he did not use the Indian numerals, had already used a placeholder (a dot) for powers of ten. Thus, he was aware of the concept of zero. And this is between 476-550 AD, clearly predating the Cambodian zero.

  Or were you speaking of the earliest inscription of zero?
  • Amir Aczel  nashv • 12 days ago

    Well, I love Aryabhatta and his work. There is also the famous Bakhshali manuscript, kept at Oxford, believed to be from the 8th to the 12th centuries--but it has never been radiocarbon dated. I concentrated on the oldest verified stone inscription (some day, maybe one will be found in India--there has been one called the Khandela Inscription, with an early zero, but no one knows where it is).
• Michael Coe • 10 days ago

  Steve Lloyd is absolutely correct. The use of zero is basic to the Maya Base 20 system of positional numeration. Amit Acad should have done more research. This is a misleading article and I'm amazed that Discovery magazine (which I admire) published such a claim. The Khmer of Cambodia were pretty amazing, but the Maya mathmeticians have priority.
  • Al West  Michael Coe • 9 days ago

    Assuming you're *the* Michael Coe, I suppose you'd know!
• Steve Lloyd • 13 days ago

  The Mayan zero is a place-holder as well, as a simple search of 'maya and zero' quickly shows. The title of the article is plainly false, and the complete omission of the in-fact earliest zero of Meso-america makes the article itself worth, as titled, zero. Don't blame the messenger, just the first of many who would have pointed this out, as your editors should have managed long ago. As it stands this article should be retracted.
  • Amir Aczel  Steve Lloyd • 12 days ago

    Mr. Lloyd,
    Your "friendly" comment probably doesn't deserve a response. We at the Crux try to have civilized discussions of science topics without ad hominem and rudeness. Internet sites can be inaccurate. The Maya zero was used in calendrical work to denote zero days or years, etc. It was different from our versatile, multi-purpose, base-10 "Hindu-Arabic" system. It was the zero of that system, and its provenance, that was the subject of my research. For the Maya zero and its purposes, see Georges Ifrah, The Universal History of Numbers, NY: Wiley, 2000, pp. 316-322.
    • Jennifer Anne Bangstrom  Amir Aczel • 10 days ago

      I feel your assessment of Mr. Lloyd is a little off base (no pun intended). Although he appears to be a colossal douche, I happen to know for fact he is only a moderate douche.
    • Ganesan  Amir Aczel • 12 days ago

      The system should be mentioned as Hindu system since Arabs only transmitted it. Nowadays, the option to copyright is available.
      • Amir Aczel  Ganesan • 10 days ago

        Yes, Al-Khowarizmi and others used the Hindu numerals--the oldest come from the Ashoka inscriptions, 3rd c. BC, and Nana Ghat cave inscriptions, near Puna, 2nd c. AD, all in India. From the Arabs, the numerals and the zero were transmitted to Europe largely by Fibonacci, but possibly earlier. A good reference is Kim Plofker, Mathematics in India, Princeton U Press, 2009
        • Chris Williams  Amir Aczel • 10 days ago

          The earliest known use of zero in Mesoamerica is in 37BCE. Zero is used not only in the long count calendar but also as a placeholder in their modified vigesimal counting system. The Olmec and Mayans had advanced mathematics for calculating astronomical events and positions of which could not have been calculated without a value assigned to their zero.

          Haughton, p. 153. The earliest recovered Long Count dated is from Monument 1 in the Maya site El Baúl, Guatemala, bearing a date of 37 BCE.

          The omission of this data reduces the validity of the article.
    • mfhussain  Amir Aczel • 10 days ago

      Steve clearly had not taken his meds with his morning tea when writing this comment. Great work on the research, you clearly know your subject matter!
    • SixSixSix  Amir Aczel • 9 days ago

      All this scholarly bickering is a zero sum game that will come to nothing. After all, all things and all people in their place.
• Tarek Jan • 13 days ago

  Actually it's "Abu Abdallah Muḥammad ibn Musa al-Khwarizmi"
• อมร อุ่นจิตต์วรรธนะ • 11 days ago

  Wikipedia, the Free Encyclopedia. Save this ancient story of the one that "Empire of the Mare (:) or Cambodian Khmer Empire or some sources that the ancient Khmer empire began around the sixth century, starting with the kingdom of Funan [1] is located in the country. Cambodia The territory covers parts of Thailand, Laos, Vietnam, and parts of present. It is a kingdom, with most power in Southeast Asia. Subsequently weakened and lost some territory to the Kingdom of Sukhothai and break eventually colonized the Ayutthaya Kingdom. Khmer kingdom of Chenla inherited power sports. Alternately, win the war turns up with side effects such as the Kingdom of Lan Xang kingdom. Ayutthaya Kingdom. Cham kingdom and spa. The most important legacy of the Khmer Empire, Angkor Wat and Angkor Thom, which was once the kingdom of Siam on this prosperity possible. There are also ideological beliefs. Variety. The main religion of the empire, including Hinduism, Mahayana Buddhism. And Theravada Buddhism, which was from Sri Lanka. On the 13th century ...
• Rajasegarampillai Suresh • 13 days ago

  You do realise that Cambodia was a heavily Indic-influenced culture at the time? The script you've 'discovered' gives that away with it's South Indian nature.
  • Amir Aczel  Rajasegarampillai Suresh • 12 days ago

    Absolutely! Georges Coedes called the civilizations of SE Asia "Indianized"--because the used Sanskrit and worshipped (at various times) the Hindu gods and Buddhism. Curiously, K-127 (this inscription) is in Old Khmer, not Sanskrit, but still many scholars (including Coedes) claimed that the discovery implied an Indian invention. With more research, time will tell!
    • sagrika  Amir Aczel • 10 days ago

      'Hindu', not Indianized?
  • Ganesan  Rajasegarampillai Suresh • 13 days ago

    This is incorrect. Tamil is the oldest language from the South. But, if you look at the Tamil script, none of the characters have any resemblance to 0. This being the case, South Indians may not have created 0. This is from the Northern(Gangetic) region only. Cambodia was very much tied with ancient India.
• Al West • 9 days ago

  'Chaka' is not the correct name of the calendar/era. Śāka is the correct transcription, normally seen as 'Saka' or 'Shaka' rather than Chaka. Earlier scholars - including, I believe, Coedes - used 'çāka', but the sound is a voiceless palato-alveolar fricative (as in 'shin') not a voiceless palatal fricative (as in German 'ich'), so Śāka is more correct.

  Also, for interest's sake: the script is Pallava, which is a South Indian script strongly associated with early first millennium Indian influence in southeast Asia. This indicates to me that the zero was probably not a Khmer invention, and instead came as part of a parcel of scribal traditions, alongside the Pallava writing system. Its absence from India at the same time is better explained by the lack of inscriptions and poor preservation of early Indian documents from the same period, which has affected Indian historiography in plenty of other ways. South Asia is a spectacularly poorly documented place before the thirteenth century.
• Steve Lloyd • 13 days ago

  You are, apparently, utterly unaware of the Maya.
  • Amir Aczel  Steve Lloyd • 13 days ago

    Not at all. The Mayan ten is a =, not one and zero next to it; and after 19 you get to powers of 20--zero is not used in that notation; the zero glyph is very different. The Cambodian zero is a place-holder, just as in our "Hindu-Arabic" numerals.
    • sagrika  Amir Aczel • 10 days ago

      Sir
      Not that it matters too much, but why call the Hindu numerals 'Arabic'? Algebra too was invented by the Hindus so isn't calling it the Arabic term, Al Gebra, enough?! LOL
    • Chris Williams  Amir Aczel • 10 days ago

      The earliest known use of zero in Mesoamerica is in 37BCE. Zero is used
      not only in the long count calendar but also as a placeholder in their 
      modified vigesimal counting system. The Olmec and Mayans had advanced 
      mathematics for calculating astronomical events and positions of which 
      could not have been calculated without a value assigned to their zero.

      As an example, the decimal value of 361 is represented by three Mayan glyphs the first and third being single dot like our period "." and the second or middle glyph would be a modified "turtle shell" representing zero (0 here for demonstration purposes.

      .
      0
      .

      . = 1 x 360
      0 = 0 x 20
      . = 1 x 1

      For a sum of 361.
      • Frank Schoeman  Chris Williams • 9 days ago

        I don't know what a "modified" base 20 system looks like, but if extend hexadecimal (base 16) with g=16, h=17, i=18, j=19, 361((18*20 +1) is represented as i1, no need for a 'zero', 401(1*20^2 + 1), on the other hand is 101 in base 20. Did you just pick a bad example because otherwise I don't see how in base 20 any number less than 400 base 10, needs 3 digits?
        • Chris Williams  Frank Schoeman • 9 days ago

          There are two number systems the Mayan use. Both are placeholder value systems using base-20 or a modified base-20.

          For arithmetic, they used a straight base-20 system throughout with a zero placeholder. This was done through a series of horizontal bars and dots stacked upon one another for values greater than zero and a "shell" of sorts for a placeholder of zero.

          Their second counting system was for the long-count calendar. This was a modified base-20 system whereas the third digit was base-18 and all the others were base-20.

          An example of their numbers is attached in the pic (if it comes over properly.)

          Looks like it didn't. I'll try another image.

          see more
          • Chris Williams  Chris Williams • 9 days ago

            Here's the image
  • Bryan Katz  Steve Lloyd • 10 days ago

    Mayan civilization peaked between 300 - 800 C.E. (AD). The first three centuries of this period corresponded to the Gupta age in India (300- c600). 
    It's pretty amazing that 2 civilizations on opposite sides of the world both invented the symbol for zero at roughly the same time.

    The predictable part is that once it was invented in India, the zero symbol spread east and west quite rapidly. In contrast, in the Americas, Mayan hieroglyphs (and the zero) remained confined to Mesoamerica - due in large part to the north-south axis of these continents.
• Edmond Cohen • 3 days ago

  Well, we all might argue the origin of the universal 0, but what's important is how the 0, the no thing became everything in modern communications. It is because the 0 is the intangible that creates the tangible through Baby Bangs occurring at the instantaneous speed of Time, where the past collides with the future, manifesting The Eternal Now (T.E.N. 010) that just past, gone into the unknown oblivion, not to be repeated (exactly) ever again. Go Baby Bangs vs. the elusive Big Bang. 
  The universe is dualistic in term of 010, as the concise equation for the unified field theory, or, the Theory Of Everything, for the next billion years.
  • Oliver  Edmond Cohen • 3 days ago

    I don't know what you're smoking, but I want the same
    • Edmond Cohen  Oliver • 8 hours ago

      Interesting how I, obviously generated a response from you about the Idea of the intangible 0 nothingness which you smoked out the understanding of. I mean understanding the Theory Of Everything as a 010 equation, it might be too simple... for lack of "Smoke"!?
      • Oliver  Edmond Cohen • 3 hours ago

        I say, you're trying to hide your lack of sense behind a smokescreen
• stevlich • 9 days ago

  There really was a Fibonacci. I thought it was a made up name, a takeoff on Liberace. And Pol Pot's name is constantly surfacing even though nobody's ever heard of him except weird history buffs.
  • bud278  stevlich • 6 days ago

    Or anyone who lived through the 1970s and paid any attention to the Khymer Rouge and current events in Southeast Asia... and I guess some weird history buffs.
• keval • 9 days ago

  "Chaka era began in the year 78 AD" Just wondering if this Chaka era is same as saka era used in india, which also starts from 78 AD.

  http://en.wikipedia.org/wiki/S...
• อมร อุ่นจิตต์วรรธนะ • 11 days ago

  This is Khmer language?
• Francisco • 13 days ago

  • −

  Great story, but you didn't mention the mayan zero

  http://blogs.discovermagazine.com/crux/2013/05/20/how-i-rediscovered-the-oldest-zero-in-history/#.Uav1UNIwevc