Āryabhaṭa and his sine table
Everyone and his son have written about Āryabhaṭa and his sine table. Yet we too do this because sometimes the situation arises where you have to explain things clearly to a layman who might have some education but is unfamiliar with the intricacies of, or in some cases lacks the correct perspective on, Hindu tradition.
Regarding him Hindu tradition states:
siddhānta-pañcaka-vidhāv api dṛg viruddham
auḍhyoparāga-mukha-khecara-cāra-kḷptau |
sūryaḥ svayaṃ kusumapury abhavat kalau tu
bhūgolavit kulapa āryabhaṭābhidhānaḥ ||
When the predictions of the five siddhānta-s and observations of conjunctions, occultations and setting times of planets began to conflict the solar deity himself incarnated in Kusumapuri in the Kali age in the form of the geographer and head professor Āryabhaṭa.
The great astronomer and mathematician Āryabhaṭa-I’s, who was seen by some Hindus as the incarnation of the solar deity, was born in 476 CE in the Aśmaka country (close to modern Maharashtra-Telangana border). He was active at Pāṭaliputra in the golden age of Hindu power during the reign of emperor Budhagupta. He is known to have composed at least two works the Āryabhaṭīya, which was an update of the old Svāyambhuva-siddhānta tradition, and the Āryabhaṭa-siddhānta which was modeled after the old Sūrya siddhānta. We are informed by Bhāskara-I that in his Āryabhaṭīya Āryabhaṭa was following in the footsteps of the great astronomer of antiquity Pārāśarya, who was likely one of the early promulgators of the Svāyambhuva tradition. Āryabhaṭa as head professor is said to have had the following notable students: Lāṭadeva, Niśaṅku, Pāṇḍuraṅgasvamin and Prabhākara. Sadly their works have been lost. Of them Lāṭadeva is recorded in old Hindu scientific tradition as having written several works including on Hellenistic astronomy and likely succeeded Āryabhaṭa as the ācārya of his school.
Thus, Āryabhaṭa’s work is the earliest surviving record of one of the most important Hindu scientific traditions, namely that of Svāyambhuva-s. In the manner of the scientists of old Hindu naturalistic tradition Āryabhaṭa presents the acquisition of scientific knowledge as the attainment of brahmavidyā:
daśa-gītika-sūtram idam bhū-graha-caritam bha-pañjare jñātvā |
graha-bha-gaṇa-paribhramaṇaṃ sa yāti bhittvā param brahma ||
Having known these sūtra-s in the ten verses composed in the gītika meter providing the motions of the Earth and the planets within the celestial sphere [pañjara: marked by the coordinate grid], and having penetrated the orbits of the planets and the stars he attains the supreme brahman.
His clear mention of the movement of the Earth in the celestial sphere along with the other planets in the celestial sphere has been taken as Āryabhaṭa’s discovery of heliocentricity. However, here we are not going into this issue and the real nature of his unique planetary model which sets the old Hindu Svāyambhuva planetary model apart from those of the Greeks. Nevertheless, as a testimony of his astronomical achievements we will merely state the period of sidereal day of the Earth as determined by Āryabhaṭa in modern units:
One of the important features of Āryabhaṭa’s work was his presentation of the old Hindu sine difference table. Āryabhaṭa gives the table using his syllable-numeral equivalence which goes as:
makhi bhaki phakhi dhakhi ṇakhi ñakhi ṅakhi hasjha skaki kiṣga śghaki kighva |
ghlaki kigra hakya dhaki kica sga jhaśa ṅva kla pta pha cha kalā ardha-jyāH ||
225, 224, 222, 219, 215, 210, 205, 199, 191, 183, 174, 164, 154, 143, 131, 119, 106, 93, 79, 65, 51, 37, 22, 7 are the
So how do we understand this? As per Hindu terminology if the arc is equivalent to the bow then the chord is equivalent to the bowstring (jyā). Hence, the sine can be seen as half a jyā (ardhajyā) as Āryabhaṭa terms it in the above sūtra. For simplicity call Āryabhaṭa’s ardhajyā a function named jyā and represent it thus in modern notation:
Let the function jyā![(\theta) (\theta)]() be defined as,
be defined as,
jyā![(\theta)=R\sin(\theta) (\theta)=R\sin(\theta)]() , where
, where ![R=3438 R=3438]() .
.
Let the function jyā
jyā
Why the number 3438? Āryabhaṭa conceives a circle whose circumference is divided into
Thus, Āryabhaṭa’s R value is for the first time a radian-like concept was used in trigonometry. Now, Āryabhaṭa divides his quadrant into 24 parts; thus, his minimal angle is
jyā ![(\dfrac{\pi}{48})=3438\sin(\dfrac{\pi}{48})=3438\times0.06540 \approx 225 (\dfrac{\pi}{48})=3438\sin(\dfrac{\pi}{48})=3438\times0.06540 \approx 225]()
Thus, Āryabhaṭa’s value of ![\theta_1 \theta_1]() is chosen such that the angle and its jyā are practically the same (Figure 1). This value as a proxy for
is chosen such that the angle and its jyā are practically the same (Figure 1). This value as a proxy for ![\displaystyle \lim_{\theta \to 0}\frac{\sin(\theta)}{\theta}=1 \displaystyle \lim_{\theta \to 0}\frac{\sin(\theta)}{\theta}=1]() continued to be used in the subsequent development of Hindu calculus. The
continued to be used in the subsequent development of Hindu calculus. The ![\theta \theta]() and jyā
and jyā ![(\theta) (\theta)]() being nearly the same at this value allows linear interpolation for intermediate values.
being nearly the same at this value allows linear interpolation for intermediate values.

Figure 1
Now the rest of his table is in the form of differences. So to get a jyā ![(\theta_n) (\theta_n)]() we have to do the following:
we have to do the following:
jyā![(\theta_2)=225+224=449 (\theta_2)=225+224=449]() ; jyā
; jyā ![(\theta_3)=225+224+222=671 (\theta_3)=225+224+222=671]() …
…
The table below compares Āryabhaṭa’s jyā![(\theta) (\theta)]() values to the exact modern values.
values to the exact modern values.
![AryabhaTa_sin]()
jyā
The table below compares Āryabhaṭa’s jyā

https://manasataramgini.wordpress.com/2017/03/19/aryabha%E1%B9%ADa-and-his-sine-table/
TRANSMISSION OF THE CALCULUS FROM KERALA TO EUROPE [1]
TheAryabhata Group[2]
School of Education Exeter and Manchester , UK
IntroductionIndia
A key point, that has not been noticed earlier, is this: these developments cannot be dismissed as “pre-calculus”, the way the works of Fermat, Pascal, Wallis, Torricelli, Roberval, etc. usually are. Thus, the traditional Indian number system, similar to the floating point numbers used in present-day computers, together with sharp estimates of the remainder or error term, enabled the Indian mathematicians to provide a rigorous rationale for the infinite series and the infinitesimal calculus.[8]This was quite unlike the case of Newton, etc. who, lacking also the notion of real number, used “fluxions” or “infinitesimals”[9], the exact meaning of which remained a mystery until the development of mathematical analysis and the clarification of the notion of “proof” in the late 19th century and early 20th century CE. Since the Indian mathematicians had a rigorous rationale which Newton
It is true that the Yuktibhasa ideas of mathematics and proof differ from the Platonic and Hilbertian idea that mathematics must be divorced from the empirical; however, it is hard to see, from either a theoretical or a practical point of view, why acceptance of the Platonic point of view and Platonic authority ought to be a key ingredient of mathematics. In particular, the Platonic insistence on a divorce from the empirical leaves hanging in the air the question of what logic ought to underlie a proof,[10]whereas acceptance of the empirical would mean a change in the notion of proof, since different criteria are used to validate a physical theory. Since this paper is concerned with transmission, rather than epistemology, we do not pursue this any further.
Prior to Vasco da Gama there is ample evidence of the import of Indian mathematical knowledge into Europe .[11]The history of Indian arithmetical techniques imported into Europe via the Arabs as “algorismus” texts is now well known. (Algorismus is the Latinized version of Al Khwarizmi (9th century CE), who translated the arithmetical and astronomical texts of the 7th century CE Brahmagupta.) These “algorismus” techniques were first introduced into Europe by Gerbert (Pope Sylvester III) in the 10th century CE, but it is only in the 16th century CE that their final triumph over abacus techniques started being depicted on the covers of arithmetical texts.[12]On the other hand, there is also, from afterthe late 17th century, ample evidence of the large scale import of Indian texts and manuscripts, tens of thousands of which are today housed in European libraries[13]. Our primary hypothesis for investigation is that this process of importing Indian texts continued also during the unstudied intervening period of the 16thand 17th century. Our general hypothesis is that the arrival of Vasco da Gama in Calicut
Further, it is our hypothesis that the epistemological difficulties encountered with infinitesimals in Europe from the 17thto the 19th centuries CE arose, exactly like the difficulties with sunya (zero), due to the import of techniques with a different epistemological base.[14]This has important pedagogical implications. However, in this paper we will set aside the epistemological and pedagogical issues and focus on the question of transmission.
What is the evidence for transmission? Before addressing this question we need to address a meta-question: what is an acceptable standardof evidence for transmission? This meta-question seems not to have been addressed at all in the literature on the history of mathematics.[15]In the past there have been far too many claims of transmission, where the evidence produced is farcical; for example, in support of the widespread claim of the transmission of Ptolemaic astronomy from Alexandria to India, one line of evidence, proposed by Thibaut, is that Varahamihira’s use of “Paulisha” suggests that it could have been derived from “Paul” (rather than Pulisha or Pulastya, one of the seven sages forming the constellation known as the Great Bear). If this be the standard of evidence, there is nothing for us to prove. For the works of Paramesvara, Madhava, Nilakantha, and Jyeshtadeva, clearly precede those of Fermat, Pascal, Gregory, Wallis, Newton , and Leibniz, and India was clearly known (and actively linked) to Europe by the 16th century CE.
However, we are aware that, for some unfathomable reasons, the standard of evidence required for an acceptable claim of transmission of knowledge from East to West is different from the standard of evidence required for a similar claim of transmission of knowledge from West to East. Priority and the possibility of contact always establish a socially acceptable case for transmission from West to East, but priority and definite contact never establish an acceptable case for transmission from East to West, for there always is the possibility that similar things could have been discovered independently. Hence we propose to adopt a legal standard of evidence good enough to hang a person for murder. Briefly, we propose to test the hypothesis on the grounds of (1) motivation, (2) opportunity, (3) circumstantial evidence, and (4) documentary evidence.
The motivation for import of knowledge derived from the needs of greater accuracy in (a) navigation, (b) the calendar, and (c) practical mathematics (used for everyday financial calculations). Christoph Clavius, a key figure in the transitional period, exhibits all three concerns: since he (a) authored a book on practical mathematics, (b) headed the calendar reform committee, and (c) was a student of the famous navigational theorist Pedro Nunes.
Navigation was clearly the key motivation, being then a matter of the greatest strategic and economic importance for Europe . Early navigators like Columbus, and Vasco da Gama did not know stellar navigation,[16]and dead reckoning was of little use in “uncharted” seas unless, like Columbus Newton
Consequently, not only kings and parliaments, but also very many of the leading scientists of the times were involved in these efforts. Galileo, for example, unsuccessfully competed for the revised Spanish prize for 16 years, before shifting his attention to the Dutch prize. Colbert wrote personally to all the leading scientists of Europe, offering large rewards, and selected from the replies received to start the French Royal Academy Newton
However, the popular accounts of the history of navigation have focussed on the development of the marine chronometer, which relates to the 18th century CE. Our concern is with navigation in the 16th and 17th centuries CE, when the focus was on stellar and celestial navigation, apart from geodesy and geography. Indeed the enormous growth of interest in mathematics and astronomy in Europe in the 16th and 17th centuries CE, is directly attributable to the practical benefit that these studies were expected to have on the navigational problem.
Secondly, the popular account of navigation history has focussed almost exclusively on the problem of longitude determination, whereas in the 16th century CE, latitude determination was the key problem, because of an inaccurate calendar, and the then lack of knowledge of celestial navigation in Europe . Latitude determination also involved a problem of timekeeping, but this timekeeping pertained to the calendarrather than the chronometer. India
What sorts of texts might the Europeans have searched for to learn more about navigation? As we saw above, stellar/solar navigation naturally related to the study of astronomy and timekeeping, which was, then, inseparably linked to mathematics. Most Indian texts on mathematics, too, were located in the context of astronomy and timekeeping. (In particular, this is true for all the texts on the calculus, mentioned above.) The term jyotisa, as in Vedanga Jyotisa, meant timekeeping.[17] Stellar astronomy and mathematics was used for timekeeping, and also for constructing the calendar.
Moreover, the navigational and calendrical knowledge that the Europeans needed and sought in ancient texts was, in fact, available in Indian mathematical and astronomical texts. The widely distributed Laghu Bhaskariya (abridged work of Bhaskara) and Maha Bhaskariya (extensive work of Bhaskara) of the first Bhaskara (629 CE) explicitly detailed methods of determining the local latitude and longitude, using observations of solar declination, or pole star altitude, and simple instruments like the gnomon, and the clepsydra.[18]Since local latitude could easily be determined from solar declination by day and e.g. pole star altitude at night (using a common instrument like the kamal), an accurate sine table was just what was required to determine local longitudefrom a knowledge of latitudinal differences and course angle. The simplest method was to solve a plane triangle. The Laghu Bhaskariya already states the criticism that determination of longitude by a calculation involving planetriangles is not adequate because of the roundness of the earth. Later texts like the Siddhanta of Vatesvara (904 CE) pointed out that these techniques needed to be corrected by applying spherical trigonometry. Al Biruni, the 10th-11th century scholar, who visited India
Exactly this technique started being tried in Europe in the 16th century, when the centre of navigational excellence in Europe had shifted from Florence to Coimbra Goa , in the 1540's during which they reportedly failed, presumably due to inaccurate techniques of calculation, inadequate sine table, and other factors listed below.
Though the Europeans, motivated by navigation, were actively seeking the knowledge of determining local latitude and longitude through stellar astronomy, and though this knowledge was available in Indian mathematical texts, there were three things that impeded their search. They lacked: (a) knowledge of practical and mental arithmetic, (b) an accurate calendar, and (c) an accurate estimate of the size of the earth. An accurate estimatew of the size of the earth was needed for the calculation of longitudes/departures, from a knowledge of only latitude differences and course angle.[24]While Caliph al Mamun had confirmed through empirical observations in the 9thcentruy CE, the estimates of the equatorial radius of the earth given in Indian astronomical texts, and al Biruni had implemented a cheaper and easier technique to confirm these,[25]Columbus
Secondly, in the first part of the 16th century lacking even an accurate calendar, and lacking techniques of calculation, the difficulty was with determining latitudecorrectly. It has been overlooked in the popular history of navigation that the longitude problem was preceded by a latitude problem. Well before the attempt to construct an accurate chronometer to solve the longitude problem, the attempt was to construct an accurate calendar to solve the latitude problem.
Thus, Vasco da Gama was unacquainted with instruments like the kamal or rapalagai used to determine latitude by measurement of pole-star altitude. This instrument was used by the Indian pilot who navigated him across the Arabian sea from Melinde in Africa to Calicut in India
While this technique was presumably mastered by the Europeans by the mid-16th century CE, this was useful only at night. The standard technique for determining latitude in day time was to use solar declination. While a great variety of instruments were available for measuring solar declination, linking solar declination to the local latitude required an accurate calendar. The European calendar, then in use, was unchanged since Roman times, and was inaccurate because it was a solar calendar which assumed that the length of the year was 365 ¼ days. Making the calendar accurate was a problem which involved the date of the equinoxes, identical with the ritual concern with the date of the Easter festival. By 1545 CE this problem had been recognised by both navigators (like Nunes) and by the church which set up a committee to review the date of Easter.
Thus, it was in this direction of correcting the calendar that the European efforts to gather knowledge were first focussed. As already stated above, the calendar, in India
How did the Europeans gather local knowledge? Were they familiar with local languages? Like al Biruni was to Mahmud of Ghazni, the Jesuits were to the Portuguese an intelligence gathering arm. The Jesuits learned the local languages like Malayalam, Telegu and Tamil[26]easily enough, and Valignano declared that it was more important for Jesuits to learn the local language than to learn philosophy. However, the Jesuits were (a) deficient in knowledge of mathematics, and (b) constrained by an inaccurate ritual calendar. Christoph Clavius, who had studied under the famous Pedro Nunes at Coimbra
Clavius also wrote a text on practical mathematics, and compiled and published a tables of sines[28]which could be looked up without the need for any mental calculation. These tables, presumably, were intended to replace the tables of Regiomontanus, taken from Arabic sources, and those of Rheticus, who perhaps also obtained his information from Arabic sources, like Copernicus.[29]Thus, Clavius recognized and strove to remove all the drawbacks listed above. The need for more accurate sine tables for navigational purposes was stressed also by Clavius’ contemporary, Simon Stevins, in his criticism of the work of Pedro Nunes. Stevins explicitly states Aryabhata’s value of p, observing that it is more accurate than that of Regiomontanus, who came nearly a thousand years after Aryabhata.[30](As is well known, Stevins contemporary, Ludolph von Ceulen devoted a lifetime to getting increasingly accurate values of p.)
(2) Opportunity Lisbon India Cochin (until the Protestant Dutch closed down the Cochin College India India
At some point in their stay in India these Jesuits went the Malabar region including the city of Cochin
As mentioned above, Ricci was in search of Indian calendrical knowledge. He and the other Jesuits could not but have noticed the discrepancy between their calendar and the local calendar. For example, the Jesuits were accustomed to the idea that festivals like Christmas fell on a fixed day of their calendar so they could not have failed to notice that the major Indian festivals like Dussehara, Diwali, Holi, Sankranti etc., did not fall on the same days of the Julian calendar. However, the typical Jesuit before Matteo Ricci probably did not know enough about astronomy to have known the difference even between the sidereal year (the basis of the Indian calendar) and the tropical year (the basis of the Julian/Gregorian calendar); so they could hardly have been expected to understand the complexities of the Indian calendar. However they could easily have acquired the knowledge in manuscript form and sent it back to either Maffei in Portugal
In India Cochin India
Finally, we emphasise that Matteo Ricci’s mathematical preparation was most suited to the task at hand. Christoph Clavius had written a commentary on the Sphere of Sacro Bosco, (after studying the Sphere of Pedro Nunes) and had published in 1580 a large 645 page book on Gnomonices. The sphere (gola) and the gnomon (shanku) were the two key topics needed to understand Indian astronomy and timekeeping: Aryabhata devotes a chapter to the sphere, while Vatesvara has a whole book on it. Ricci had studied nautical science along with the Cosmographia of Apian, so he could hardly have missed the significance and importance of precise sine values. The latter Jesuits such as Schreck and Rubino were just as qualified to undertake this mission to acquire knowledge[36].
Ricci went to Cochin Cochin
We emphasise that the Jesuits had much more than a casual interest in India Cochin India
(3) The Scenario of Transmission
Before we move on to the documentary evidence for transmission to Europe of the calculus that had developed in India Europe . Europeans, particularly Jesuits, had ample opportunity to access the texts and calendrical almanacs in which this information was to be found, not only in the straightforward sense that they knew the local languages well, but also in the sense that trained mathematicians were sent for the express purpose of collecting the knowledge available in these texts.
Let us now turn to detail the circumstantial and documentary evidence, for it helps also to understand how this knowledge, after arriving in Europe, diffused in Europe . (Apart from historical curiosity, this is also a matter of contemporary pedagogical significance, since it enables us to assess, in a non-destructive way, the possible impact of introducing today the study of calculus with a different epistemological basis.)
We know too little even to conjecture anything about the accumulation of knowledge in Coimbra, nor exactly what happened to this accumulated knowledge after Jesuits took over control of the university after about 1560. After 1560, in line with the above reasoning, our working hypothesis, or scenario, is that over a 50 year period, say from 1560 to 1610, knowledge of Indian mathematical, astronomical and calendrical techniques accumulated in Rome, and diffused to nearby universities like Padova and Pisa, and to wider regions through Cavalieri and Galileo, and through visitors to Padova, like James Gregory[37]. Subsequently, it also reached Paris where, through the agency of Mersenne, and his study circle, it diffused throughout Europe .
Mersenne, though a minim monk, had received a Jesuit education, and was closely linked to Jesuits. Mersenne’s correspondence reveals that Goa and Cochin Europe . (Newton India , without the intervention of Rome
(3) Circumstantial Evidence
With this scenario as the background, we can ask: what sort of circumstantial evidence can we hope to find? Certainly it would be absurd to expect citations in published work! The tradition in Europe of that time was that mathematicians did not reveal their sources. When they could get hold of others’ sources, they copied them without compunction. The case of e.g. Cardan is well known, and there are well documented cases against, e.g. Copernicus,[42]Galileo[43], Descartes[44], etc., of copying from others, whether or not such copying amounted to “plagiarism”. Under these circumstances, mathematicians naturally kept their sources a closely guarded secret: they published only problems, not their solutions, and challenged other mathematicians to solve them.
(a) Fermat and Pell’s Equation.England ![]() , where A is any nonsquare integer.”[45]Mathematicians in
, where A is any nonsquare integer.”[45]Mathematicians in Europe were unable to solve Fermat’s challenge problem for over 75 years, until Euler published a general solution in 1738. In February 1657, Fermat also wrote a letter to Frenicle, where he elaborated upon this problem:[46]“What is for example the smallest square which, multiplied by 61 with unity added, makes a square?”
As Struik further notes, Indian mathematicians had a solution to this problem. In fact, strangely enough, exactly the case of A=61 is given as a solved example in the BeejGanitatext of Bhaskara II. This coincidence is not trivial when we consider that the solution x = 1766319049, y = 226153980 involves rather large numbers.[47]A similar problem had earlier been suggested by the 7th century Brahmagupta, and Bhaskara II provides the general solution with his chakravala method. Thus, Fermat’s challenge problem, strongly suggests a connection of Fermat with Indian mathematics: Fermat probably had access to some Indian mathematical texts like the BijaGanita.
Euler certainly knew about Indian astronomy (hence mathematics), for Giovanni Cassini, then the most reputed astronomer of France, had already published an account of “Hindu astronomy” in 1691, and Euler wrote on the “Hindu year”[48] (sidereal year; the pope’s bull was still not acceptable e.g. to Protestant Britain, until 1752). Since numerous Indian astronomical texts deal with “Pell’s” equation, Euler had presumably learnt about this as well. However, we are not aware that he acknowledged this when he published his solution to what he called Pell’s equation.
This suggestion that Fermat knew something about Indian mathematics is reinforced by Fermat’s friendship not only with Mersenne, but with Jacques de Billy (1602-1669), a Jesuit teacher of mathematics in Dijon
 , where A is any nonsquare integer.”[45]Mathematicians in
, where A is any nonsquare integer.”[45]Mathematicians in (b) Fermat, Pascal and the Calculus
“One of Fermat’s most stunning achievements,” continues Aczel, “was to develop the main ideas of calculus, which he did thirteen years before the birth of Sir Isaac Newton [in 1642].” Fermat’s and Pascal’s approach to the calculus reinforces the belief in a connection with Indian mathematics. It was at Mersenne’s place that Pascal met Descartes who remarked in his La Geometrie of 1637 about the impossibility of measuring the circumference of a circle: “The ratios between straight and curved lines
However, in Indian mathematics, from the time of the sulba sutras, because of the different epistemological base, measuring the length of a curved line by laying a rope (sulba) along it, and straightening it (or measuring a general area by triangulation) has been quite an acceptable process, used to obtain a value of p. In fact, Aryabhata states that the area of a general plane figure should be obtained by triangulation,[50]before going on to give an improved measure of the (curved) circumference of a circle in terms of the diameter (a straight line), in the next verse.[51]In the very next verse he explains how his sine table is derived by approximating small arcs by line segments.[52] It is therefore quite natural to find this eventually developing into the calculus in the Tantrasangraha, whose author Nilakantha belonged to the Aryabhata school, and wrote wrote a lengthy commentary on the Aryabhatiya, almost exactly a thousand years after it.
Nilakantha’s younger contemporary, Jyeshtadeva, author of the Malayalam Yuktibhasa (“Discourse on Rationales”), has a chapter on the circle, explaining the method of deriving the improved sine table stated in the Tantrasangraha. The key step in this derivation[53]is the evaluation of:
![]()
This is also exactly the approach to calculus adopted by Fermat, Pascal, Wallis, etc. to evaluate the area under the parabolas ![]() , or, equivalently, calculate
, or, equivalently, calculate ![]() As Pascal remarked, about this formula, it serves to solve all sorts of problems of the calculus. “Any person at all familiar with the doctrine of indivisibles will perceive the results that one can draw from the above for the determination of curvilinear areas. Nothing is easier, in fact, than to obtain immediately the quadrature of all types of parabolas and the measures of numberless other magnitudes.” This formula has been attributed to Fermat in 1629; Roberval, another member of Mersenne’s circle, also worked on it. Earlier Cavalieri, a student of Galileo, had stated this formula, without proof, in 1635, after waiting five years for Galileo to write on infinitesimals. John Wallis, who visited
As Pascal remarked, about this formula, it serves to solve all sorts of problems of the calculus. “Any person at all familiar with the doctrine of indivisibles will perceive the results that one can draw from the above for the determination of curvilinear areas. Nothing is easier, in fact, than to obtain immediately the quadrature of all types of parabolas and the measures of numberless other magnitudes.” This formula has been attributed to Fermat in 1629; Roberval, another member of Mersenne’s circle, also worked on it. Earlier Cavalieri, a student of Galileo, had stated this formula, without proof, in 1635, after waiting five years for Galileo to write on infinitesimals. John Wallis, who visited Pisa
The curious thing is that though so many European mathematicians seem to have suddenly “discovered” this formula at about the same time, the formula had no natural epistemological basis in European mathematics, either of that time or for the next two centuries, for European mathematics was oriented towards “proof” rather than “calculation”, and shared the Greek “horror of the infinite”. Even today, despite the compelling changes of technology, due to widespread use of supercomputers, the situation has not entirely changed, and as in the time of Clavius, calculation continues to be regarded as “inferior” to “proof”.
Though the European mathematicians were unable to prove the above formula or provide a rigorous rationale for it within their epistemology,[54]even the techniques by which they attempted to prove the formula suggests transmission. For example, Pascal tried to establish[55]the formula using the so-called Pascal’s triangle, for the binomial coefficients. The triangle appears as the meru prastara, in Pingala’s Chandahsutra of (-3 century CE ), and another 1200 years later in the work of his 10th century CE commentator Halayudha.[56]It was known to the Arabs and the Chinese.[57]Among Renaissance European mathematicians it is found in the arithmetic of Apian, and in the work of authors like Bombelli[58].
(c) The Ahargana and the Julian Day-Number System
Now, from at least the time of Aryabhata, all dates in Indian astronomy are specified in this way, using day numbers. This eliminates any possible ambiguity due to calendrical differences; such ambiguities did exist because of the variety of calendars in use. These day numbers are specified as Ahargana or “heap of days”. Understanding the first stanza of the Aryabhatiyarequires us to know about this system; in fact, the day number system could have been transmitted by absolutely any Indian astronomical text.
The difference between Ahargana and Julian day numbers is only this: the Aharganacount starts from the beginning of the Kaliyuga, (17 Feb -3102 CE) whereas the Julian day-number count starts from 1 Jan - 4713 CE (an astronomically convenient date, presumably related to the date of Biblical creation). Thus, the Aharganadiffers from the Julian day number by exactly 588,465 which is the Julian day number for the start of the Kaliyuga. Of course, the system is simple enough and could have been invented by anyone at any time. The strange thing is that the system was allegedly invented in Europe at exactly the time, in 1582, when it could have been transmitted through a stated earlier desire to learn about Indian calendrical techniques. If our conjecture about transmission of the day-number system is true, it would seem that well before their conquest of Cochin , the Dutch had independent sources of information from India
 |
 , or, equivalently, calculate
, or, equivalently, calculate  As Pascal remarked, about this formula, it serves to solve all sorts of problems of the calculus. “Any person at all familiar with the doctrine of indivisibles will perceive the results that one can draw from the above for the determination of curvilinear areas. Nothing is easier, in fact, than to obtain immediately the quadrature of all types of parabolas and the measures of numberless other magnitudes.” This formula has been attributed to Fermat in 1629; Roberval, another member of Mersenne’s circle, also worked on it. Earlier Cavalieri, a student of Galileo, had stated this formula, without proof, in 1635, after waiting five years for Galileo to write on infinitesimals. John Wallis, who visited
As Pascal remarked, about this formula, it serves to solve all sorts of problems of the calculus. “Any person at all familiar with the doctrine of indivisibles will perceive the results that one can draw from the above for the determination of curvilinear areas. Nothing is easier, in fact, than to obtain immediately the quadrature of all types of parabolas and the measures of numberless other magnitudes.” This formula has been attributed to Fermat in 1629; Roberval, another member of Mersenne’s circle, also worked on it. Earlier Cavalieri, a student of Galileo, had stated this formula, without proof, in 1635, after waiting five years for Galileo to write on infinitesimals. John Wallis, who visited (d) Planetary Models and Elliptic Orbits
There are many other key instances that should count as circumstantial evidence. For example, Nilakantha’s planetary model, in the Tantrasangraha, is exactly the “Tychonic” model (Tycho was a contemporary of Clavius), except that it involves elliptical orbits. (It is now known that Tycho’s student, Kepler, obtained his elliptical orbits by computing his “observations”.[59]) We do not go into these for reasons of space, since we first need to give an exposition of all the relevant planetary theories.
(4) Documentary Evidence of the Role of the Jesuits
The period after Vasco da Gama’s arrival in Calicut in 1498 and the establishment, shortly thereafter, of a Portuguese colony with bases in Cochin , Cannanore and Goa, by Afonso de Albuquerque in 1510, laid the foundations for Catholic missionary work in the Malabar coast .
Among the various missions, the Jesuit one was the most important in respect of transmitting local knowledge to Europe . While there is a paucity of literature on this subject (mainly due to the, as yet, uncatalogued nature of a vast quantity of oriental manuscripts in Portugal
The earlier Jesuits in the Malabar Coast were interested in arithmetic, astronomy and timekeeping is indicated by many references in the Documenta Indica[62]. Their interest in local science seems motivated also indirectly by their policy to master vernacular languages such as Malaylam and Tamil[63]so much so that they were encouraged to speak to each other in the vernacular to progress this policy. Prominent Jesuits who became fluent native speakers included De Nobili who spoke Sanskrit and Tamil (the language spoken in Trichur) and the Portuguese Diogo Gonsalves who spoke Malayalam fluently. The attempt by Jesuits to learn the vernacular was so widespread that they frequently used Malayalam to sign their names in letters to the Society of Jesus headquarters in Rome Malabar Coast .[66]The Jesuits’ study of the vernacular languages was not merely intended to facilitate their work in conversions. It was also intended to enable work on transmitting this knowledge back to Europe . This is supported by the acquisition of translations of Malyalam and Sanskrit manuscripts[67]. Further evidence of this knowledge acquisition is contained in the ARSI collections Goa 38, 46 and 58. The last being the work of Diogo Gonsalves and contains detailed notes on the judicial system and on the sciences and mechanical arts of the Malabar region. In addition the Jesuit Luis Frois who worked in the Malabar region is referred to in Goa 46 was active in information acquisition[68]. Then there is de Menses who, writing from Kollam in 1580, reports that, on the basis of local knowledge, the European maps have inaccuracies[69].
The arrival of Matteo Ricci in Goa in September 13, 1578 , as pointed out earlier, was significant in respect of Jesuit acquisition of local knowledge. His specialist knowledge of mathematics, cosmography, astronomy and navigation made him a candidate for discovering the knowledge of the colonies and he had specific instructions to investigate the science of India
“…had resided in the cities of Goa and of Cochin for more than three years and a half (September 13, 1578-April 15, 1582): he had been requested to apply himself to the scientific study of this new and imperfectly know country, in order to document his illustrious contemporary, Father Maffei, the ‘Titus Livius’ of Portuguese explorations.”[70]
Bernard reports that Ricci had begun his task prior to arriving in India
There were other later Jesuits who report of scientific findings on such diverse things as calendrical sciences and inaccuracies in the European maps and mathematical tables. Antonio Rubino writes, in 1610, similarly about inaccuracies in European mathematical tables[72]. Then there is the letter from Schreck, in 1618, of astronomical observations intended for the benefit of Kepler[73]- the latter had requested the eminent Jesuit mathematician Paul Guldin to help him to acquire astronomical knowledge from India
Further, the Jesuits established printing presses all over the Malabar region; in 1550 in Goa which used Roman types, in 1577 in Vaipicota using Tamil and Malyalam types, in 1602 Vaipicota using Syro-Chaldic, and in 1578 in Tuticorin with Tamil types. The aim of these presses was to publish the catechism so essential for missionary work; for example, St Francis Xavier’s catechism was published in 1557 by the Goa press. The aim was also to translate the local science into Portuguese prior to transmission to Europe; for example, Garcia da Orta’s Colloquios dos simples e drogas he cousas mediçinas da India published in Goa in 1563[75]. There were many other publications of this type but they remain obscure because, as Sarton points out “A Portuguese book printed in Goa could not attract much attention outside the Portuguese world.”[76]Nevertheless, subsequent Jesuits such as Schreck followed on from Garcia da Orta in botany[77].
All available evidence points out that the Jesuits were active in acquiring local scientific knowledge including astronomy and calendrical science. Thus they would have been aware of the astronomy of the Madhava school and would have sought it out. But how might the Jesuits have obtained key manuscripts of Indian astronomy such as the Tantrasangraha and the Yuktibhasa? We present a plausible conjecture. Such manuscripts would require the Jesuits being in close contact with scholarly Brahmins; there is concrete evidence that they were in contact with such people. There is plenty of evidence of the Jesuits being in contacts with kings across the country. We establish that the Jesuits had close relations with the kings of Cochin
The kings of Cochin
This suggests that the former royal family in Cochin Cochin Portugal
Given this close relationship with the Kings of Cochin, the Jesuit desire to know about local knowledge, and the royal family’s contiguity to the works on Indian astronomy, it is quite possible that the Jesuits may have acquired the key manuscripts via the royal household. In addition after the 1580 annexation of Portugal by Spain and subsequent loss of funding from Lisbon Europe of the calculus that had developed in the works of the mathematicians and astronomers of the Aryabhata school between the 14th and 16th centuries. We established strong motivation for the transmission in the needs of navigation and the calendar reform., which were recognised as the most important scientific problems of that age in Europe . We also established that Europeans had ample opportunity to access the texts and calendrical almanacs in which this information was to be found not only in the straightforward sense that they knew the local languages well, but also in the sense that trained mathematicians were sent for the express purpose of collecting the knowledge available in these texts. The circumstantial evidence for transmission would appear while the work on documentary evidence has only just started.
ENDNOTES
[1] This paper is based on a presentation at the ‘International Conference on 1500 years of the Aryabhateeyam’, Thiruvanthapuram , India
[2]The Aryabhata Group acknowledges financial support from the School of Education , University of Exeter
[3] A.P. Jushkevich, Geschichte der Matematik im Mittelater German translation, Leipzig, 1964, Moscow Calcutta India , Chaukhambha Orientalia, Delhi Taylor
[4] The version of the TantraSangrahawhich has been recently serialised (K. V. Sarma ed) together with its English translation (V. S. Narasimhan Tr.) in the Indian Journal of History of Science (issue starting Vol. 33, No. 1 of March 1998) is incomplete and does not contain the relevant passages. We have used the verion of the TantraSangraha as found in the TantraSangrahaVyakhya, Palm Leaf MS No 697 and its transcript No. T 1251, both of the Kerala University MS Library, Trivandrum
[5] P. K. Koru (ed) Karana-paddhati of Putumuna Somayaji, Astro Printing and Publishing Co., Cherp (Kerala), 1953, p 203; S. K. Nayar (ed) Karana Paddhati of Putumuna Somayaji, Govt. Oriental Manuscript Library, Madras, 1956, pp 189--193. For an exposition, see C. K. Raju, “Kamal or Rapalagai”, Paper presented at the Xth Indo-Portuguese Conference on History, Indian National Science Academy, New Delhi, Dec 1998.
[7] J. Warren, Kala Sankalita, Madras Britain and Ireland
[8] C. K. Raju, “Computers, Mathematics Education, and the Alternative Epistemology of the Calculus in the YuktiBhasa”, Plenary talk: Session on Technology, Education, and Changing Conceptions of Knowledge, 8th East-West conference, Hawai’i
[9] For example in J.F.Scott, The Mathematical Work of John Wallis, Chelsea , New York
[10] This is not an empty question since the logic employed in other cultural traditions, like the empirical logic of quantum mechanics, need be neither 2-valued nor even truth functional; see, C. K. Raju, “Mathematics and Culture”, in: History, Time and Truth: Essays in Honour of D. P. Chattopadhyaya, (eds) Daya Krishna and K. Satchidananda Murty, Kalki Prakash, New Delhi 1998.
[11] Suzan Rose Benedict, A Comparative Study of the Early Treatises Introducing into Europe the Hundu Art of Reckoning, Ph.D. Thesis, University of Michigan, April, 1914, Rumford Press.
[12] The victory of algorismus over abacus was depicted by a smiling Boethius using Indian numerals, and a glum Pythagoras to whom the abacus technique was attributed. This picture first appeared in the Margarita Philosophica of Gregor Reisch, 1503, and is reproduced e.g. in Karl Menninger, Number Words and Number Symbols: A Cultural History of Numbers, (Tr) Paul Broneer, MIT Press, Cambridge, Mass., 1970, p 350. According to the periodisation suggested by Menso Folkerts, the abacus period commenced by the 12th century, though the use of the abacus is obviously much older. Menso Folkerts, Lecture at the Second Meeting of the International Laboratory for the History of Science, Max Planck Institute for the History of Science, Berlin
[13] An early descriptive catalogue of the Indian manuscripts in the Vatican Rome
[14] For the different epistemology underlying the notion of sunya, see C. K. Raju, “Mathematical Epistemology of Sunya”, summary of interventions at the Seminar on the Concept of Sunya, Indian National Science Academy and Indira Gandhi Centre for the Arts, Delhi, Feb, 1997. To appear in Proceedings.
[15] See, however, C. K. Raju, “India China West Asia in Mathematics and Astronomy” in A. Rahman (ed) India China West Asia , PHISPC, New Delhi India
[18] Specifically, the method of determining longitude using a clepsydra is detailed in Laghu Bhaskariya , II.8 (Ed and Tr. K. S. Shukla), Department of Mathematics and Astronomy, Lucknow University
[19] E. S. Kennedy, A Commentary Upon Biruni’s Kitab Tahdid al Amakin, An 11th Century Treatise on Mathematical Geography, American University Beirut Beirut
[20] J. Carvalho, Pedro Nunes – Defensaõ Do Tratado Da Rumacao Do Globo Para A Arte De Navegar, Coimbra, 1952
[21] D. J. Struik, A Source Book in Mathematics, 1200--1800, Harvard University Cambridge , Mass.
[22]The Principal Works of Simon Stevin, Vol. III, Astronomy and Navigation (eds) A Pannekoek and Ernst Crone, Amsterdam, Swets and Seitlinger, 1961.
[23] For a figure etc., see C. K. Raju, “Kamal...” cited above. Stevins, The Haven Finding Art, cited above, p 481 et. seq. Nunes ascribed to the loxodrome a particular property, viz. That the sines of the polar distances of the points of intersection with meridians at equal differences of longitude form a continued proportion. Stevins,(p 491) refuted this by direct calculation.
[24] For more details, see C. K. Raju, “Kamal...” cited above
[25] For details of Al Biruni’s technique, and for the connection to the Indo-Arabic navigational measure of zam, see C. K. Raju, “Kamal or Rapalagai,” cited earlier.
[26] See, for example, D. Ferroli, The Jesuits in Malabar, Bangalore
[28] Christophori Clavii Bambergensis, Tabulae Sinuum, Tangentium et Secantium ad partes radij 10,000,000 ..., Ioannis Albini, 1607. As the title suggests, this table concerns not sine values proper, as today understaood, but RSine values which are what are given in Indian manuscripts. Stevins follows the same practice for his secant tables, The Haven Finding Art, cited above, p 483.
[29] George Saliba, A History of Arabic Astronomy in the Golden Age of Islam,New York University
[30]The Principal Works of Simon Stevins, Vol III, cited above, p 603.
[31] V.Cronin, in The Wise Man From The West – Matteo Ricci and His Mission To China, Fount, Collins, 1984, p 22, states that “. ….. in 1575 Ricci entered a new phase of his studies; philosophy and mathematics, Aristotle and Euclid. The advanced course was taught by a young German, Christopher Clavius, the most brilliant mathematician of his day. …He showed special aptitude for this course winning notice as a mathematician of promise.”
[32]Isaia Iannaccone, Johann Schreck Terrentius, Instituto Universitario Orientale, Napoli, 1998
[33] See, for example, Ugo Baldini, Studi Su Filosofia E Scienza Dei Gesuiti In Italia 1540 - 1632, Bulzoin Editore, 1992
[34] See, for example, D. Ferroli, The Jesuits in Malabar, Bangalore
[35] Printing has somewhat simplified this process. For a listing of 60 different currently printed pancanga-s, see Report of the Calendar Reform Committee, Govt of India, CSIR, 1955.
[36]Ugo Baldini, Studi su filosofia e scienza dei gesuiti in Italia 1540 - 1632, Bulzoni Editore, 1992, p70 “Si può ricordare che molti dei migliori allievi gesuiti di Clavio e Geienberger (iniziando con Matteo Ricci e proseguendo con C. Spinola, G. Aleni, G. A. Rubino, S. De Ursis, Schreck, G. Rho) divennero missionari nelle Indie orientali. Questa scelta, se li fece protagonisti di un interscambio tra la tradizione europea e quelle indiana e cinese, particolarmente in matematica ed astronomia, che fu di per sé un fenomeno di grande significato storico, limitò certamente la loro produttività scientifica.”
[37] See H W Turnbull , James Gregory Tercentenary Memorial Volume, London Italy Padua London Italy
[38]Correspondance du P. Marin Mersenne, 18 volumes, Presses Universitaires de France, Paris, 1945-. ; A letter from the astronomer Ismael Boulliaud to Mersenne in Rome, Vol XIII, p 267-73.
[39]Correspondance, Vol XIII, p 518-521.
[40]Correspondance, Vol II, p 103-115.
[41] E.g. Carl B. Boyer, A History of Mathematics, Wiley, 1968, p 424; C. H. Edwards, The Historical Development of the Calculus, Springer, 1979, p 113.
[42] George Saliba, cited earlier.
[43] William Wallace, Galileo and his Sources – The heritage of the Collegio Romano in Galileo’s Science, Princeton University Press, 1984,has direct evidence of Galileo borrowing heavily from Jesuit sources in the Collegio Romano.
[44] Fauvel and Gray, The History of Mathematics – A Reader, Macmillan, 1987, p 291, describe Wallis’s strong claim that Descartes plagiarized a treatise of Thomas Harriot (Britain Newton
[45] D. Struik, A Source Book in Mathematics, cited earlier, p 29.
[46] D. Struik, A Source Book in Mathematics, cited above, p 30.
[47] For an modern introduction to details of Bhaskara’s chakravala method, see I. S. Bhanu Murthy, A Modern Introduction to Ancient Indian Mathematics, Wiley Eastern, new Delhi
[48] Euler’s paper on the “Hindu year” was an appendix to Historia Regni Graecorum Bactriani by T. S. Bayer; see G. R. Kaye, Hindu Astronomy, 1924, reprinted, Cosmo Publications, 1981, p 1.
[49] Amir D. Aczel, Fermat’s Last Theorem, Penguin, p 5.
[50]Ganita, 9 a-b. Aryabhatiya of Aryabhata,(ed and Tr.) K. S. Shukla and K. V. Sarma, Indian National Science Academy Delhi
[52]Ganita, 11. Aryabhatiya, cited above.
[53] C. K. Raju, “Approximation and proof in the Yuktibhasa derivation of Madhava’s sine series”, cited earlier.
[54] E..g. Cavalieri’s statement is now termed a conjecture, while Wallis is said to have stated the formula without proof. Edwards, cited above, p 114; Boyer, cited above, p 417.
[55] E.g. Edwards, cited above, p 109-113.
[56] S. N. Sen, “Mathematics”, in D. M. Bose, S. N. Sen, and B. V. Subbarayappa (eds), A Concise History of Science in India Indian National Science Academy Delhi
[57] Photographs of a 1303 Chinese depiction of Pascal’s triangle have been provided by Joseph Needham, The Shorter Science & Civlisation in China, Vol 2, Cambridge University Press, 1981, p 55.
[58] Bombelli acknowledged the transmission of Indian mathematics to the West. From J. Fauvel and J. Gray, The History of Mathematics, Macmillan, 1987, we have (page 264) from the preface of Bombelli's Algebra“ …a Greek work on this discipline has been discovered in the Vatican Rome
[59]“Planet fakery exposed. Falsified data: Johannes Kepler” The Times (London 25 January 1990 , 31a, including large excerpts from the article by William J. Broad, “After 400 years, a challenge to Kepler: He fabricated his data, scholars say”. New York Times23 January 1990 , C1, 6. The key article is William Donahue, “Kepler’s fabricated figures: Covering up the mess in the New Astronomy” Journal for the History of Astronomy, 19 (1988) p 217-37.
[60] E.g. Gérard Colas, Les manuscrits envoyé de l’Inde par les jésuites français entre 1729 et 1735, Bibliothèque nationale de France, Paris.
[61] O. Spies, “Il P. Calmette e le sue Conoscenze Indologiche”, Studia Indologica, Bonn, 1955, p 53- 64.
[62] See, for example, Documenta Indica, IV p 293 and VIII p 458.
[63]Documenta Indica, XIVp 425 and XV p 34*, and D. Ferroli, The Jesuits in Malabar, Bangalore
[64] see, e.g., the letters contained in the manuscript collection Goa 13 at the Archivum Romanicum Societate Iesu in Rome
[66] Documenta Indica, III, p 307
[67] For example, D. Ferroli, The Jesuits in Malabar, 1939, Vol 2, p402, states “In Portuguese India, hardly seven years after the death of St. Francis Xavier the fathers obtained the translation of a great part of the 18 Puranas and sent it to Europe . A Brahmin spent eight years in translating the works of Veaso (Vyasa)……several Hindu books were got from Brahmin houses, and brought to the Library of the Jesuit college. These translations are now preserved in the Roman Archives of the Society of Jesus. (Goa 46)”
[68] Luis Pina, As Ciencias Na Historia Do Imperio Colonial Portugueses, (seculos XV a XIX), Lisbon como
[69]Documenta Indica XI, P185, a letter of de Menses, Coulano, dated 31/12/1580 states “Lá mando a V.P. huma descripçam de todo o mundo por muitos astrologos apurada e pilotos, e quanto ás cousas da india, sem nenhum erro nas alturas e schalas miliharias, por se fazer por astrologos e pilotos que cada dia correm estas terras, porque as cartas de lá sam todas erradas nas alturas indicas, como eu claramente vi.”
[70] Henri Bernard, Matteo Ricci’s Scientific Contribution to China, Hyperion Press, Westport , Conn.
[71]“Com tudo não me parece que sera impossivel saberse, mas has de ser por via d`algum mouro honorado ou brahmane muito intelligente que saiba as cronicas dos tiempos, dos quais eu procurarei saber tudo.” Letter by Matteo Ricci to Petri Maffei on 1 Dec 1581. Goa38I, ff 129r--30v, corrected and reproduced in Documenta Indica, XII, 472-477 (p 474). Also reproduced in Tacchi Venturi, Matteo Ricci S.I., Le Lettre Dalla Cina 1580-1610, vol 2, Macerata, 1613.
[72] Ugo Baldini, Studi su filosofia e scienza dei gesuiti in Italia 1540 - 1632, Bulzoin Editore, 1992, p214reports of Rubino’s letter “…….scritta da una località indiana il cui nome è di lettura incerta, egli informa di fare rilevazíoni per cartografare il territorio, per determinare alcune posizioni si è servito di eclissi, confrontando i tempi locali reali con quelli desumibili dalle efemeridi di Magini e riscontrandovi grandi inesattezze; chiede perciò altre efemeridi, oppure le Tabulae prutenicae.”
[73] See, Isaia Iannaccone, Johann Schreck Terrentius, Instituto Universitario Orientale, Napoli, 1998,
[74] C. Baumgardt, Johannes Kepler: Life and Letters, Philosophical Library, NY, 1951, p 153, (in Kepler’s letter to Paul Guldin Jesuit professor of mathematics in Vienna Linz India India
[76] D. Sarton, 1955, The Appreciation of Ancient and Medieval Science During the Renaissance (1450-1600), University of Pennsylvania
[77] See Isaia Iannaccone, Johann Schreck Terrentius, Instituto Universitario Orientale, Napoli, 1998
[78] C. M. Whish, On the Hindu Quadrature of the Circle…., Transactions of the Royal Asiatic Society of Great Britain Ireland Calcutta
[79]YuktibhasaPart 1, with notes (Ed) Ramavarma (Maru) Tampuran and A. R. Akhileswara Aiyar, Mangalodayam Ltd, Trichur, 1948 (in Malayalam). Most subsequent work has relied on this exposition.
[80] In a personal communication with, Mukunda Marar, the eldest son of the last king of Cochin the Aryabhata Group has established that the former kings were, at the least, all aware of the astronomical methods of the astrological prediction and of the MS that contained these methods. Several were scholarly enough to publish commentaries of the mathematical/astronomical works. Mukunda Marar, himself, worked with C T Rajagopal and published a work On the Hindu Quadrature of the Circle, Journal of the Royal Asiatic Society (Bombay
[81] see for example, Documenta Indica, X, pages 239, 834, 835, 838, and 845
[82]Documenta Indica,XV, p 224
[83]Documenta Indica, vol XV, p 7*
[84]Documenta Indica, vol XV, p 667
[85] “Most of the Jesuit missionaries set to work to master the vernaculars…. some of their number studies Indian books and Indian philosophy, not merely with the idea of refuting it, but with the desire of profiting by it.” D. Ferroli, The Jesuits in Malabar, 1939, volume 2, p 93.
[1] This paper is based on a presentation at the ‘International Conference on 1500 years of the Aryabhateeyam’, Thiruvanthapuram , India
[2]The Aryabhata Group acknowledges financial support from the School of Education , University of Exeter
[3] A.P. Jushkevich, Geschichte der Matematik im Mittelater German translation, Leipzig, 1964,
of the original, Moscow Calcutta India , Chaukhambha Orientalia, Delhi Taylor
[4] The version of the TantraSangrahawhich has been recently serialised (K. V. Sarma ed) together with its English translation (V. S. Narasimhan Tr.) in the Indian Journal of History of Science (issue starting Vol. 33, No. 1 of March 1998) is incomplete and does not contain the relevant passages. We have used the verion of the TantraSangraha as found in the TantraSangrahaVyakhya, Palm Leaf MS No 697 and its transcript No. T 1251, both of the Kerala University MS Library, Trivandrum
[5] P. K. Koru (ed) Karana-paddhati of Putumuna Somayaji, Astro Printing and Publishing Co., Cherp (Kerala), 1953, p 203; S. K. Nayar (ed) Karana Paddhati of Putumuna Somayaji, Govt. Oriental Manuscript Library, Madras, 1956, pp 189--193. For an exposition, see C. K. Raju, “Kamal or Rapalagai”, Paper presented at the Xth Indo-Portuguese Conference on History, Indian National Science Academy, New Delhi, Dec 1998.
[6] K. V. Sarma (Ed and Tr) GanitaYuktiBhasa of Jeyshtadeva (Analytical Exposition of the Rationales of Indian Mathematics and Astronomy), unpublished typescript , p 33-34. The precise number of decimal places actually calculated should not be used as a yardstick of development, since the method used was such higher precision values could be obtained with only slightly greater effort. Thus, the number of correct decimal places actually obtained in the expansiion of p should be taken as an index of requirement rather than capability.
[7] J. Warren, Kala Sankalita, Madras Britain and Ireland
[8] C. K. Raju, “Computers, Mathematics Education, and the Alternative Epistemology of the Calculus in the YuktiBhasa”, Plenary talk: Session on Technology, Education, and Changing Conceptions of Knowledge, 8th East-West conference, Hawai’i
[9] For example in J.F.Scott, The Mathematical Work of John Wallis, Chelsea , New York
P 66 we see that “Wallis [in A Defense of the Treatise of the Angle of Contact] introduced the idea of ‘inceptive quantities’, and his definition of these – prima principia quod sic – no doubt provided Newton with a hint for the ‘nascent quantities’ which are at the root of the Method of Fluxions. ‘There are some things’, said Wallis, ‘which tho’ as to some kind of Magnitude, they are nothing; yet are in the next possibility of being somewhat. They are not in it, but tantum non; they are in the next possibility to it; and the beginning of it….’”
[10] This is not an empty question since the logic employed in other cultural traditions, like the empirical logic of quantum mechanics, need be neither 2-valued nor even truth functional; see, C. K. Raju, “Mathematics and Culture”, in: History, Time and Truth: Essays in Honour of D. P. Chattopadhyaya, (eds) Daya Krishna and K. Satchidananda Murty, Kalki Prakash, New Delhi 1998.
[11] Suzan Rose Benedict, A Comparative Study of the Early Treatises Introducing into Europe the Hundu Art of Reckoning, Ph.D. Thesis, University of Michigan, April, 1914, Rumford Press.
[12] The victory of algorismus over abacus was depicted by a smiling Boethius using Indian numerals, and a glum Pythagoras to whom the abacus technique was attributed. This picture first appeared in the Margarita Philosophica of Gregor Reisch, 1503, and is reproduced e.g. in Karl Menninger, Number Words and Number Symbols: A Cultural History of Numbers, (Tr) Paul Broneer, MIT Press, Cambridge, Mass., 1970, p 350. According to the periodisation suggested by Menso Folkerts, the abacus period commenced by the 12th century, though the use of the abacus is obviously much older. Menso Folkerts, Lecture at the Second Meeting of the International Laboratory for the History of Science, Max Planck Institute for the History of Science, Berlin
[13] An early descriptive catalogue of the Indian manuscripts in the Vatican Rome
[14] For the different epistemology underlying the notion of sunya, see C. K. Raju, “Mathematical Epistemology of Sunya”, summary of interventions at the Seminar on the Concept of Sunya, Indian National Science Academy and Indira Gandhi Centre for the Arts, Delhi, Feb, 1997. To appear in Proceedings.
[15] See, however, C. K. Raju, “India China West Asia in Mathematics and Astronomy” in A. Rahman (ed) India China West Asia , PHISPC, New Delhi
[16] For references and other details see C. K. Raju, “Kamal or Rapalagai” Paper presented at the Xth Indo-Portuguese meeting on History, Indian National Science Academy, Dec 1998, to appear in Proc. The rapalagai was the instrument used by the Indian pilot who brought Vasco da Gama to India
[17] Later on the term jyotisacame to mean the determination of more specifically auspicious or “lucky” times for performing rituals, so that jyotisais today often mistranslated as astrology, “astral science”, etc.
[18] Specifically, the method of determining longitude using a clepsydra is detailed in Laghu Bhaskariya , II.8 (Ed and Tr. K. S. Shukla), Department of Mathematics and Astronomy, Lucknow University
[19] E. S. Kennedy, A Commentary Upon Biruni’s Kitab Tahdid al Amakin, An 11th Century Treatise on Mathematical Geography, American University Beirut Beirut
[20] J. Carvalho, Pedro Nunes – Defensaõ Do Tratado Da Rumacao Do Globo Para A Arte De Navegar, Coimbra, 1952
[21] D. J. Struik, A Source Book in Mathematics, 1200--1800, Harvard University Cambridge , Mass.
[22]The Principal Works of Simon Stevin, Vol. III, Astronomy and Navigation (eds) A Pannekoek and Ernst Crone, Amsterdam, Swets and Seitlinger, 1961.
[23] For a figure etc., see C. K. Raju, “Kamal...” cited above. Stevins, The Haven Finding Art, cited above, p 481 et. seq. Nunes ascribed to the loxodrome a particular property, viz. That the sines of the polar distances of the points of intersection with meridians at equal differences of longitude form a continued proportion. Stevins,(p 491) refuted this by direct calculation.
[24] For more details, see C. K. Raju, “Kamal...” cited above
[25] For details of Al Biruni’s technique, and for the connection to the Indo-Arabic navigational measure of zam, see C. K. Raju, “Kamal or Rapalagai,” cited earlier.
[26] See, for example, D. Ferroli, The Jesuits in Malabar, Bangalore
[27] It is noteworthy that Nunes had, in 1577 received an invitation to join the commission on the reform of the calendar. See J. Carvalho, Pedro Nunes – Defensaõ Do Tratado Da Rumacao Do Globo Para A Arte De Navegar, Coimbra, 1952, p x.
[28] Christophori Clavii Bambergensis, Tabulae Sinuum, Tangentium et Secantium ad partes radij 10,000,000 ..., Ioannis Albini, 1607. As the title suggests, this table concerns not sine values proper, as today understaood, but RSine values which are what are given in Indian manuscripts. Stevins follows the same practice for his secant tables, The Haven Finding Art, cited above, p 483.
[29] George Saliba, A History of Arabic Astronomy in the Golden Age of Islam,New York University
[30]The Principal Works of Simon Stevins, Vol III, cited above, p 603.
[31] V.Cronin, in The Wise Man From The West – Matteo Ricci and His Mission To China, Fount, Collins, 1984, p 22, states that “. ….. in 1575 Ricci entered a new phase of his studies; philosophy and mathematics, Aristotle and Euclid. The advanced course was taught by a young German, Christopher Clavius, the most brilliant mathematician of his day. …He showed special aptitude for this course winning notice as a mathematician of promise.”
[32]Isaia Iannaccone, Johann Schreck Terrentius, Instituto Universitario Orientale, Napoli, 1998
[33] See, for example, Ugo Baldini, Studi Su Filosofia E Scienza Dei Gesuiti In Italia 1540 - 1632, Bulzoin Editore, 1992
[34] See, for example, D. Ferroli, The Jesuits in Malabar, Bangalore
[35] Printing has somewhat simplified this process. For a listing of 60 different currently printed pancanga-s, see Report of the Calendar Reform Committee, Govt of India, CSIR, 1955.
[36]Ugo Baldini, Studi su filosofia e scienza dei gesuiti in Italia 1540 - 1632, Bulzoni Editore, 1992, p70 “Si può ricordare che molti dei migliori allievi gesuiti di Clavio e Geienberger (iniziando con Matteo Ricci e proseguendo con C. Spinola, G. Aleni, G. A. Rubino, S. De Ursis, Schreck, G. Rho) divennero missionari nelle Indie orientali. Questa scelta, se li fece protagonisti di un interscambio tra la tradizione europea e quelle indiana e cinese, particolarmente in matematica ed astronomia, che fu di per sé un fenomeno di grande significato storico, limitò certamente la loro produttività scientifica.”
[37] See H W Turnbull , James Gregory Tercentenary Memorial Volume, London Italy Padua London Italy
[38]Correspondance du P. Marin Mersenne, 18 volumes, Presses Universitaires de France, Paris, 1945-. ; A letter from the astronomer Ismael Boulliaud to Mersenne in Rome, Vol XIII, p 267-73.
[39]Correspondance, Vol XIII, p 518-521.
[40]Correspondance, Vol II, p 103-115.
[41] E.g. Carl B. Boyer, A History of Mathematics, Wiley, 1968, p 424; C. H. Edwards, The Historical Development of the Calculus, Springer, 1979, p 113.
[42] George Saliba, cited earlier.
[43] William Wallace, Galileo and his Sources – The heritage of the Collegio Romano in Galileo’s Science, Princeton University Press, 1984,has direct evidence of Galileo borrowing heavily from Jesuit sources in the Collegio Romano.
[44] Fauvel and Gray, The History of Mathematics – A Reader, Macmillan, 1987, p 291, describe Wallis’s strong claim that Descartes plagiarized a treatise of Thomas Harriot (Britain Newton
[45] D. Struik, A Source Book in Mathematics, cited earlier, p 29.
[46] D. Struik, A Source Book in Mathematics, cited above, p 30.
[47] For an modern introduction to details of Bhaskara’s chakravala method, see I. S. Bhanu Murthy, A Modern Introduction to Ancient Indian Mathematics, Wiley Eastern, new Delhi
[48] Euler’s paper on the “Hindu year” was an appendix to Historia Regni Graecorum Bactriani by T. S. Bayer; see G. R. Kaye, Hindu Astronomy, 1924, reprinted, Cosmo Publications, 1981, p 1.
[49] Amir D. Aczel, Fermat’s Last Theorem, Penguin, p 5.
[50]Ganita, 9 a-b. Aryabhatiya of Aryabhata,(ed and Tr.) K. S. Shukla and K. V. Sarma, Indian National Science Academy Delhi
[51]Ganita, 10. Aryabhatiya, cited above.
[52]Ganita, 11. Aryabhatiya, cited above.
[53] C. K. Raju, “Approximation and proof in the Yuktibhasa derivation of Madhava’s sine series”, cited earlier.
[54] E..g. Cavalieri’s statement is now termed a conjecture, while Wallis is said to have stated the formula without proof. Edwards, cited above, p 114; Boyer, cited above, p 417.
[55] E.g. Edwards, cited above, p 109-113.
[56] S. N. Sen, “Mathematics”, in D. M. Bose, S. N. Sen, and B. V. Subbarayappa (eds), A Concise History of Science in India Indian National Science Academy Delhi
[57] Photographs of a 1303 Chinese depiction of Pascal’s triangle have been provided by Joseph Needham, The Shorter Science & Civlisation in China, Vol 2, Cambridge University Press, 1981, p 55.
[58] Bombelli acknowledged the transmission of Indian mathematics to the West. From J. Fauvel and J. Gray, The History of Mathematics, Macmillan, 1987, we have (page 264) from the preface of Bombelli's Algebra“ …a Greek work on this discipline has been discovered in the
Library of our Lord in the Vatican Rome
[59]“Planet fakery exposed. Falsified data: Johannes Kepler” The Times (London 25 January 1990 , 31a, including large excerpts from the article by William J. Broad, “After 400 years, a challenge to Kepler: He fabricated his data, scholars say”. New York Times23 January 1990 , C1, 6. The key article is William Donahue, “Kepler’s fabricated figures: Covering up the mess in the New Astronomy” Journal for the History of Astronomy, 19 (1988) p 217-37.
[60] E.g. Gérard Colas, Les manuscrits envoyé de l’Inde par les jésuites français entre 1729 et 1735, Bibliothèque nationale de France, Paris.
[61] O. Spies, “Il P. Calmette e le sue Conoscenze Indologiche”, Studia Indologica, Bonn, 1955, p 53- 64.
[62] See, for example, Documenta Indica, IV p 293 and VIII p 458.
[63]Documenta Indica, XIVp 425 and XV p 34*, and D. Ferroli, The Jesuits in Malabar, Bangalore
[64] see, e.g., the letters contained in the manuscript collection Goa 13 at the Archivum Romanicum Societate Iesu in Rome
[65] V. Cronin, A Pearl to India – The Life of Roberto de Nobili, Darton, Longman and Todd, 1966, p 178-180.
[66] Documenta Indica, III, p 307
[67] For example, D. Ferroli, The Jesuits in Malabar, 1939, Vol 2, p402, states “In Portuguese India, hardly seven years after the death of St. Francis Xavier the fathers obtained the translation of a great part of the 18 Puranas and sent it to Europe . A Brahmin spent eight years in translating the works of Veaso (Vyasa)……several Hindu books were got from Brahmin houses, and brought to the Library of the Jesuit college. These translations are now preserved in the Roman Archives of the Society of Jesus. (Goa 46)”
[68] Luis Pina, As Ciencias Na Historia Do Imperio Colonial Portugueses, (seculos XV a XIX), Lisbon como
[69]Documenta Indica XI, P185, a letter of de Menses, Coulano, dated 31/12/1580 states “Lá mando a V.P. huma descripçam de todo o mundo por muitos astrologos apurada e pilotos, e quanto ás cousas da india, sem nenhum erro nas alturas e schalas miliharias, por se fazer por astrologos e pilotos que cada dia correm estas terras, porque as cartas de lá sam todas erradas nas alturas indicas, como eu claramente vi.”
[70] Henri Bernard, Matteo Ricci’s Scientific Contribution to China, Hyperion Press, Westport , Conn.
[71]“Com tudo não me parece que sera impossivel saberse, mas has de ser por via d`algum mouro honorado ou brahmane muito intelligente que saiba as cronicas dos tiempos, dos quais eu procurarei saber tudo.” Letter by Matteo Ricci to Petri Maffei on 1 Dec 1581. Goa38I, ff 129r--30v, corrected and reproduced in Documenta Indica, XII, 472-477 (p 474). Also reproduced in Tacchi Venturi, Matteo Ricci S.I., Le Lettre Dalla Cina 1580-1610, vol 2, Macerata, 1613.
[72] Ugo Baldini, Studi su filosofia e scienza dei gesuiti in Italia 1540 - 1632, Bulzoin Editore, 1992, p214reports of Rubino’s letter “…….scritta da una località indiana il cui nome è di lettura incerta, egli informa di fare rilevazíoni per cartografare il territorio, per determinare alcune posizioni si è servito di eclissi, confrontando i tempi locali reali con quelli desumibili dalle efemeridi di Magini e riscontrandovi grandi inesattezze; chiede perciò altre efemeridi, oppure le Tabulae prutenicae.”
[73] See, Isaia Iannaccone, Johann Schreck Terrentius, Instituto Universitario Orientale, Napoli, 1998,
p58 “Durante la sosta a Goa, Schreck fu altresi impegnato in campo astronomico: assieme a Kirwitzer, Schall von Bell, Rho e Rubino annotò le osservazioni di alcune comete visibili verso la fine del 1618; i risultati di queste osservazioni furono poi inviate in Europa ai confratelli Ziegler e Decker del Collegio di Ingolstadt, affinché le trasmettessero a Kepler
[74] C. Baumgardt, Johannes Kepler: Life and Letters, Philosophical Library, NY, 1951, p 153, (in Kepler’s letter to Paul Guldin Jesuit professor of mathematics in Vienna Linz India
[75] T. J. S. Patterson, ‘Science and Medicine in India
[76] D. Sarton, 1955, The Appreciation of Ancient and Medieval Science During the Renaissance (1450-1600), University of Pennsylvania
[77] See Isaia Iannaccone, Johann Schreck Terrentius, Instituto Universitario Orientale, Napoli, 1998
[78] C. M. Whish, On the Hindu Quadrature of the Circle…., Transactions of the Royal Asiatic Society of Great Britain Ireland Calcutta
[79]YuktibhasaPart 1, with notes (Ed) Ramavarma (Maru) Tampuran and A. R. Akhileswara Aiyar, Mangalodayam Ltd, Trichur, 1948 (in Malayalam). Most subsequent work has relied on this exposition.
C. T. Ragagopal and M. S. Rangachari, ‘On an Untapped Source of Medieval Keralese Mathematics’, Archive for the History of Exact Sciences, 18, 1978, 89-102. Rajagopal and Rangachari state that Rama Varma Tampuran supplied them with the manuscript material [Desa Mangalatta Mana MS of TantraSangrahaVyakhya] relating to Kerala mathematics. Also K. V. Sarma, A History of the Kerala School of Hindu Astronomy, Hoshiarpur Vishveshvaranand Institute, 1972. On page 12, K. V. Sarma points to the valuable notes added to the analysis of Kerala astronomy by Rama Varma Maru Tampuran in his 1948 exposition of the first part of the Yuktibhasa. His subsequent translation of the Yuktibhasa has utilised the same material (personal communication).
[80] In a personal communication with, Mukunda Marar, the eldest son of the last king of Cochin the Aryabhata Group has established that the former kings were, at the least, all aware of the astronomical methods of the astrological prediction and of the MS that contained these methods. Several were scholarly enough to publish commentaries of the mathematical/astronomical works. Mukunda Marar, himself, worked with C T Rajagopal and published a work On the Hindu Quadrature of the Circle, Journal of the Royal Asiatic Society (Bombay
[81] see for example, Documenta Indica, X, pages 239, 834, 835, 838, and 845
[82]Documenta Indica,XV, p 224
[83]Documenta Indica, vol XV, p 7*
[84]Documenta Indica, vol XV, p 667
[85] “Most of the Jesuit missionaries set to work to master the vernaculars…. some of their number studies Indian books and Indian philosophy, not merely with the idea of refuting it, but with the desire of profiting by it.” D. Ferroli, The Jesuits in Malabar, 1939, volume 2, p 93.
See: https://en.wikipedia.org/wiki/%C4%80ryabha%E1%B9%ADa's_sine_table
https://en.wikipedia.org/wiki/Madhava%27s_sine_table
https://en.wikipedia.org/wiki/Bhaskara_I%27s_sine_approximation_formula
http://www.insa.nic.in/writereaddata/UpLoadedFiles/IJHS/Vol37_2_1_BNNAchar.pdf Āryabhaṭa and the table of Rsines by BN Narahari Achar Indian Journal of History of Science, 37.2 (2002) 95-99
How calculus was appropriated from India into Europe? – Dr. Bhaskar Kamble
The development of the infinitesimal calculus is considered to be a watershed event in the history of science and mathematics. Its importance in the natural sciences cannot be overestimated. Among the people credited for its invention are John Wallis (1616-1703 CE), Isaac Newton (1642-1727 CE), and Gottfried Leibniz (1646-1716 CE).
Very roughly speaking, calculus handles those problems where the rate at which ‘something’ is increasing is itself changing in time. Simple examples can include the case where the speed (the rate at which the distance is increasing) is changing in time, or the case where the acceleration (the rate at which the speed is changing in time) is changing in time. Together with Newton’s three laws of motion, which are physical in content, it offers a powerful tool to mathematically describe physical phenomena.
However, the standard story of calculus being developed in Europe independently by Newton and Leibniz, which is so universally accepted today, may well be in need of a major revision. Just like the concept of zero and the decimal number system originated in India, it is now well known that the concept of calculus also originated in India three centuries before it first appeared in Europe [1,2]. There is strong circumstantial evidence to suggest that these ideas and concepts were systematically appropriated by the church in Europe at the end of the 16th century and subsequently passed off as a European invention.
The earliest notion of calculus, specifically differential calculus, is to be found in the notion of tatkalika gati (Sanskrit: instantaneous velocity), of Bhaskaracharya (1114-1185 CE), in his monumental work Siddhanta Shiromani. In this text, he explicitly demonstrates and makes use of the relation
which is a standard result of differential calculus, to determine the instantaneous velocity of a planet. He also states one of the most important results of differential calculus – that the derivative vanishes at the points of minima or maxima, and also states what is today known as the Rolle’s theorem in analysis/calculus [2].
The tradition of mathematics in India has a long and hoary past, with several shining names such as Aryabhata, Bhaskara I, Bhaskaracharya, Brahmagupta, Varahamihira, and so on. The schools started by several of these mathematicians would constantly develop and improve upon the discoveries of the earlier mathematicians, and come up with significant new results in the process. The most sophisticated insights and developments undoubtedly come from the work of what is known as the Kerala school of mathematics, which was extant from 1300-1600 CE. They wrote commentaries on the works of earlier mathematicians such as Aryabhata and Bhaskara, and made important discoveries in what is known today as calculus. That these mathematicians developed calculus 300 hundred years before Newton and Leibniz did is obvious [1,2], but what is more interesting is how and why their work was hauled off to Europe, plagiarized, and passed off as a European invention. In this post I will try to shed light on how this occurred.
Till the 15th – 16th centuries, it is important to remember that the church dominated all spheres of life in Europe. Central to its aims was the establishment of Christianity throughout the world and destroy all ‘pagan’ and ‘heathen’ cultures in the process. The genocide of Red Indians in the Americas, or of aborigines in Australia, or Hindus in India (especially the Goa inquisition in the 16th century), are a direct consequence of these aims, and so are the continued attempts of today by Christian missionaries to convert people of other faiths into Christianity. To further these expansionist policies, it was necessary to go to far-away lands and ‘civilize’ and Christianize the ‘natives’. To do so, however, needed navigational skills which, in turn, needed a good knowledge of astronomy (for example while navigating with the help of the stars) and a good knowledge of trigonometry (for example to calculate the latitude and longitude). In particular, trigonometric tables of the sine and cosine functions are a must for accurately determining the latitude at sea based on the altitude of the pole star.
There was another very important reason why the church needed astronomical knowledge – to carry out the calendar reform. The calendar originally used by the church was the Julian calendar, which had an error of one day in a century. This error was accumulating over the centuries and was causing the date of Easter to drift further and further away from the spring equinox into summer. It was very important for the church to set it right. A good calendar is also essential for good navigation, and thus the problem of navigation and the calendar were closely related. Thus, the issues of navigation and the calendar were high priority programs by the church, and several mathematicians involved with the church were actively involved in finding solutions. Attractive prizes were offered to anyone who could come up with solutions to these problems. The most important member in this regard is Christoph Clavius, who modified the curriculum of the priests in Collegio Romano to teach them mathematics, and himself designed the mathematical content of the curriculum, as well as writing a text book on mathematics to be used by the priests in their education.
In spite of this, as is well known, European astronomy and mathematics of those times was hopelessly lacking in the required knowledge [3]. And at the same time, the astronomical and mathematical knowledge of India was much superior to that of Europe. The works of several Indian mathematicians were well known in Europe, thanks to Arabic translations of Sanskrit texts, and the subsequent translations into Latin [4]. Also Fibonacci had introduced the Indian number system to Europe in 1202 CE. The navigational skills of Indian merchants was also something of a legend [5].
To realize just how advanced the Indian mathematics was at this time, we need to look at the achievements of the Kerala school. The tradition of the Kerala school was started by Madhava of Sangamagrama (1340-1425 CE), who was followed by several brilliant mathematicians and astronomers which include Parameshvara (1380-1460 CE), Nilakantha Somayaji (1444-1544 CE), and Jyeshthadeva (1500-1610 CE). Madhava is credited with many of the discoveries of the Kerala school, but verly little of his writings survive. The results obtained by him are further elaborated and developed by later scholars such as Nilakantha Somayaji in his work Tantra Sangraha, and Jyeshthadeva in his work Yukti Bhasha. The Yukti Bhasha is a veritable text book of calculus, and offers detailed explanations of most of the results obtained by the Kerala scholars. The scholars of this school also made several astronomical observations and collected the data in their works, and proposed significant improvements of the then prevailing astronomical models. Among the achievements of the Kerala school are the systematic development of the ‘limit’ procedure, which is so central to calculus, the systematic analysis of inifinte series, infinite series expansions of the sine, cosine and arctan functions, (the so-called Taylor series of today), a plethora of series expansions of pi (including the one known today as the Gregory series, 300 years before Gregory discovered them), important contributions in spherical trigonometry, and the development of much improved astronomical models based on actual observations. A practical application, much sought after by European navigators, was the calculation of sine tables, which had been carried out by Madhava up to an accuracy of eight decimal places [6,7]. An interesting application of this work was the calculation of pi up to 17 decimal places, which is coded beautifully through the kattapayadi system in the Sadratnamala of Shankara Varman. In fact many of the works of these mathematicians are still subjects of active research by modern mathematicians! And of course, behind this there was a whole body of work by earlier Indian mathematicians such as Aryabhata, Bhaskara I and II, Brahmagupta etc.
It is in the light of this vastly superior Indian mathematics and astronomy, and the tremendous eagerness of the church to possess this knowledge, that the situation in Europe in the 15th – 16th centuries must be viewed. As already mentioned, Christoph Clavius had set up the mathematical syllabus of the Jesuit priests, and in 1578, the first batch of the most capable priests trained by him, which included Matteo Ricci, Johann Schreck, and Antonio Rubino, were dispatched to the Malabar region of Kerala, including Cochin, which was the epicenter of the Kerala mathematics.
Once they were there, they set up a printing press, learnt the local language, and gained the patronage and trust of the local scholars and royal personages. And now began in earnest the task to acquire Indian texts, translate them, and dispatch them back to Europe [7]. However, all this was kept a top secret. Even today, if you make a Google search on Matteo Ricci, you will never find the real reason why he was there, although it will be mentioned that he was in Kerala. And this, in spite of the fact Ricci and Rubino have been recorded in correspondence as answering requests for astronomical information from Kerala sources [8].
However, there is enough circumstantial evidence to prove that the transfer of the calculus from India indeed took place. First, there is little doubt about the real intention behind the trip of the Jesuits to Kerala: before being sent to India in 1578, not only were they trained in mathematics by the leading astronomer of those days, Christoph Clavius, but also that, soon thereafter in 1582, the Gregorian calendar reform took place [9]! Remember that the calendar reform was one of the pressing concerns of the church and, what is more, the committee that carried out this reform was also headed by Christoph Clavius!
Next, as mentioned already, the Kerala mathematicians had created extensive tables of sines and cosines to a high degree of accuracy. Now, in 1607, Clavius published these tables under his name, without explaining how he carried out the calculations [10]! This again leaves no doubts as to the source of these tables.
The above two circumstances are quite strong to come to the conclusion that the Europeans surreptitiously used the Kerala texts, but there is more. At the end of the 16th century, the Danish astronomer Tycho Brahe came up with his ‘Tychonic model’ of planetary motion, wherein Mercury, Venus, Mars, Jupiter and Saturn revolve around the sun, but the sun is revolving around the earth. What is interesting to note here is that this is exactly the model proposed by Nilakantha in his Tantra Sangraha some 300 years earlier [11]! What a ‘coincidence’! Remember that Tycho Brahe in the capacity of the Royal astronomer of the Holy Roman Empire had easy access to all the Kerala texts sent by missionaries such as Ricci. He was also known to be extremely secretive and jealous about the astronomical observations and other documents in his possession [11]. The only explanation and conclusion is that Brahe was in possession of the work of the Kerala school of mathematics which he used to come up with his ‘Tychonic model’.
We must also mention that Jyeshthadeva’s Yuktibhasha gives a formula involving a passage to infinity to calculate the area under a parabola. The same formula was used by Fermat, Pascal, and Wallis [8]. Wallis is also given partial credit for the development of calculus. It is thus quite safe to conclude that the Kerala texts fell into the hands of these mathematicians, based on whose work Newton and Leibniz came up with the ideas of calculus. The possibility that Newton and Leibniz had direct access to these texts cannot be ruled out.
Finally the question may be raised as to why the church kept all this activity so secret. The answer is obvious: the church could not possibly carry out its noble mission of ‘civilizing pagan cultures’ and at the same time accept that these cultures had a much advanced scientific culture upon which it (the church) was so dependent! This only makes sense since it is difficult for a ‘superior’ race to cope with the fact that an ‘inferior’ race can have a civilization and culture much more advanced than theirs. This is the reason why the Aryan race theory was created by the European imperialists when the antiquity and culture of the Hindu civilization was discovered [12]. Moreover, in the case of the church, anyone who professed to be using ‘pagan’ sources of knowledge ran the certain risk of being a heretic and being burnt at the stake for ‘devil-worship’. This certainly was a good enough incentive for anyone to conceal the true sources of knowledge! In this context, it is instructive to read the following quote from [13]:
“There is nothing ‘natural’ or universal in hiding what one has learnt from others: the Arabs, for instance, did not mind learning from others, and they openly acknowledged it. This is another feature unique to the church: the idea that learning from others is something so shameful that, if it had to be done, the fact ought to be hidden. Therefore, though the church sought knowledge about the calendar, specifically from India, and profusely imported astronomical texts … this import of knowledge remained hidden.”
Since the modern world is fortunately not governed by ecclesiastical restrictions anymore, and since it is good scientific practice to give credit where it is due, it is time that we revise the standard story of calculus and honor and remember its original inventors from Bharat.
References:
[1] ‘On the Hindu quadrature of the circle, and the infinite series of the proportion of the circumference to the diameter exhibited in the four Sastras, the Tantra Sangraham, Yucti Bhasha, Carana Padhati, and Sadratnamala’, by C. M. Whish, published in the Transactions of the Royal Asiatic Society of Great Britain and Ireland, Vol. 3, No. 3, pp. 509–523.
[2] Encyclopedia of the history of science, technology and medicine in non-western cultures (two volumes), ed. Helaine Selin, Springer.
[3] To understand the status of European navigation in the 16th century, look up Navigation, Maths and Astronomy: the Pagan Knowledge, by D. P. Agrawal ( http://www.indianscience.org/essays/15-%20E–Navigation%20&%20Math.pdf ).
[4] In this context we note how the modern names for the trigonometric functions ‘sine’ and ‘cosine’ originated: “When Arabic writers translated his (Aryabhata’s) works from Sanskrit into Arabic, they referred it as jiba. However, in Arabic writings, vowels are omitted, and it was abbreviated as jb. Later writers substituted it with jaib, meaning “pocket” or “fold (in a garment)”. (In Arabic, jiba is a meaningless word.) Later in the 12th century, when Gherardo of Cremona translated these writings from Arabic into Latin, he replaced the Arabic jaib with its Latin counterpart, sinus, which means “cove” or “bay”; thence comes the English sine” (http://en.wikipedia.org/wiki/Aryabhata#Trigonometry).
[5] One of the best kept secrets of Western history is that Vasco da Gama and Columbus were no good navigators at all. It is commonly assumed that Vasco da Gama ‘discovered’ India- he did nothing of the sort. In fact he was safely escorted to India by an Indian merchant from Gujarat, named Kanha, from the African coast.
[6] See for example http://en.wikipedia.org/wiki/Madhava’s_sine_table
[7] C.K. Raju (2007). Cultural foundations of mathematics: The nature of mathematical proof and the transmission of calculus from India to Europe in the 16 thc. CE. History of Philosophy, Science and Culture in Indian Civilization. X Part 4. Delhi: Centre for Studies in Civilizations. pp. 114–123.
[8] D. F. Almeida and G. G. Joseph, Eurocentrism in the history of mathematics: the case of the Kerala school, Race and Class, Vol. 45(4): 45-59 (2004).
[9] Resulting in the so-called Gregorian calendar, which is the one used today.
[10] Christophori Clavii Bambergensis, Tabulae Sinuum, Tangentium et Secantium ad partes radij 10,000,000 (Ioannis Albini, 1607), as quoted in C. K. Raju, Teaching mathematics with a different philosophy, Part 2: Calculus without Limits, Science and Culture 77(7-8) (2011) pp. 280-285.
[11] C. K. Raju, Ending Academic Imperialism: a Beginning. Available online at http://www.ckraju.net/papers/Academic-imperialism-final.pdf
[12] An excellent account of the Aryan race theory is given in Breaking India, by Rajiv Malhotra and Aravindan Neelakandan.
[13] D. P. Agrawal, Navigation, Maths and Astronomy: the Pagan Knowledge. The article can be accessed at http://www.indianscience.org/essays/15-%20E–Navigation%20&%20Math.pdf
http://www.indicstudies.us/PROC14.PS.pdf Astronomical Dating of Events & Select Vignettes from Indian History Volume I Edited and compiled by Kosla Vepa (2008)
http://ckraju.net/blog/?p=6 Aryabhata and Ptolemy. How does Aryabhata’s value of pi compare with Ptolemy’s?
What are some unknown facts about Aryabhata?
2 Answers
These facts are not 'unknown' but many people are unaware of them:
1. The correct spelling of Aryabhata is Aryabhata (as you have spelt it). Aryabhata is often misspelt as Aryabhatta. The meaning of 'bhata' is 'slave, soldier' whereas the meaning of 'bhatta' is 'Brahmin, learned man'. However, in all commentaries of Aryabhata by mathematcians from his school, his name is always mentioned as Aryabhata and not Aryabhatta. However, Aryabhata is often drawn as a Brahmin man wearing a sacred thread including in textbooks. There is no evidence that Aryabhata was a Brahmin and hence these pictures are wrong portrayals of Aryabhata. For more information on this, consult books by C.K.Raju. Most of the information below is also from C.K.Raju.
2. The first clear description of relativity was given by Aryabhata. (From : A Note on Aryabhata's Relativity, Parakh) The following stanzas appear in the Astronomical Section of Aryabhatiya:
Just as a man in a boat moving sees the stationary objects (on either side of the river) as moving backward, just so are the stationary starts seen by people at Lanka (reference co-ordinate on the equator), as moving exactly towards the west.
(It so appears as if) the entire structure of the asterisms together with the planets were moving exactly towards the west of Lanka, being constantly driven by the provector wind, to cause their rising and setting.
3. Aryabhata gave algorithms to compute square roots and cube roots.
4. Aryabhata gave an approximation of the value of pi correctly to five significant figures as 3.1416.
5. Aryabhat was only 23 years old when he wrote the Aryabhatiya.
6. The Madhava school or Keralese schoolin Cochin who developed calculus considered themselves as Aryabhata school, that is they were followers of his tradition of mathematics.
7. It is important to understand Aryabhata's work in the larger context of Indian mathematical tradition which is algorithmic and practical. This was necessitated because the primary source of wealth in India was agriculture and navigation. For agriculture, a way to predict monsoons was needed and for navigation trigonometry was needed. Thus, arithmetic, algebra, trigonometry and calculus were developed in India. Aryabhatiyam is important in this context because it is the oldest known book on mathematics in India.
8. I will add more points to this later.
1. The correct spelling of Aryabhata is Aryabhata (as you have spelt it). Aryabhata is often misspelt as Aryabhatta. The meaning of 'bhata' is 'slave, soldier' whereas the meaning of 'bhatta' is 'Brahmin, learned man'. However, in all commentaries of Aryabhata by mathematcians from his school, his name is always mentioned as Aryabhata and not Aryabhatta. However, Aryabhata is often drawn as a Brahmin man wearing a sacred thread including in textbooks. There is no evidence that Aryabhata was a Brahmin and hence these pictures are wrong portrayals of Aryabhata. For more information on this, consult books by C.K.Raju. Most of the information below is also from C.K.Raju.
2. The first clear description of relativity was given by Aryabhata. (From : A Note on Aryabhata's Relativity, Parakh) The following stanzas appear in the Astronomical Section of Aryabhatiya:
Just as a man in a boat moving sees the stationary objects (on either side of the river) as moving backward, just so are the stationary starts seen by people at Lanka (reference co-ordinate on the equator), as moving exactly towards the west.
(It so appears as if) the entire structure of the asterisms together with the planets were moving exactly towards the west of Lanka, being constantly driven by the provector wind, to cause their rising and setting.
3. Aryabhata gave algorithms to compute square roots and cube roots.
4. Aryabhata gave an approximation of the value of pi correctly to five significant figures as 3.1416.
5. Aryabhat was only 23 years old when he wrote the Aryabhatiya.
6. The Madhava school or Keralese schoolin Cochin who developed calculus considered themselves as Aryabhata school, that is they were followers of his tradition of mathematics.
7. It is important to understand Aryabhata's work in the larger context of Indian mathematical tradition which is algorithmic and practical. This was necessitated because the primary source of wealth in India was agriculture and navigation. For agriculture, a way to predict monsoons was needed and for navigation trigonometry was needed. Thus, arithmetic, algebra, trigonometry and calculus were developed in India. Aryabhatiyam is important in this context because it is the oldest known book on mathematics in India.
8. I will add more points to this later.
'Unknown'? No. 'Lesser-known?' Maybe.
Aryabhatta is credited with inventing an alphabetic system of notation.
These were denominations - each 10 times the preceding one - and were used for enumerating the numerical portions of his study in astronomy.
The denominations were: eka, dasa, sata, sahasra, ayuta, niyuta, prayata, koti, arbuda, and vrinda.
This laid the foundation of what came to be known in Mathematics as place value.
https://www.quora.com/What-are-some-unknown-facts-about-Aryabhata
- K.V. Sarma, Aryabhatiya of Aryabhata (critical edition with English translation and notes), 1974-76. Published by INSA, 1976, on the occasion of the 1500th Brith Anniversary Celebration of Aryabhata.
- K.V. Sarma, Aryabhatiya of Aryabhata (with commentary of Suryadeva Yajvan, critical edition), 1974-76. Published by INSA, 1976,on the occasion of the 1500th Birth Anniversary Celebration of Aryabhata. http://insaindia.res.in/comproj96.php
https://arxiv.org/ftp/arxiv/papers/1312/1312.2100.pdf Teaching mathematics with a different philosophy by CK Raju (2011)
http://www.hbcse.tifr.res.in/episteme/episteme-1/allabs/rajuabs.pdf Math wars and the epistemic divide in Mathematics by CK Raju (1999)
http://www.hbcse.tifr.res.in/episteme/episteme-1/allabs/rajuabs.pdf Math wars and the epistemic divide in Mathematics by CK Raju (1999)
https://www.youtube.com/watch?v=IaodCGDjqzs Published on Nov 20, 2015 Calculus: The Real Story - Prof. C. K. Raju (1:03:57)
MONDAY 26 OCTOBER 2009
History and Philosophy of Mathematics: C K Raju
Excerpts of this interview appeared in:
Ghadar Jari Hai—The Revolt Continues, Vol III, No. 3&4, July-Dec, 2009
Peepul ke Neeche
“Indian mathematics is practical whereas the European is metaphysical”
C K Raju has been arguing passionately through several lectures and books about the uniqueness of ancient Indian mathematics and how it influenced the rest of the world. He says what is taught as standard modern mathematics today, is based on theological positions taken by the Church after the Crusades. Shivanand Kanavi conversed with Raju on the results of his research in the history and philosophy of mathematics.
Shivanand: Dr Raju welcome to peepul ke neeche conversation. Having looked at some of your writings, I see that you have researched deeply into the mathematical tradition of India as well as that of Persia, Arabia and Europe. Could you give us an overview of exchanges between India and West Asia in the field of mathematics?
Raju: As I have stated in the book (Is Science Western in Origin?—C K Raju), the process of exchange with Arabs started with Barmakids (barmak from pramukh, Persian-Buddhists who were wazirs to Abbasid Khalifas--Ed), this was around 8th century CE, after the conquest of Persia by the Arabs. Besides the spread of Islam in Persia, Persian customs spread to the Arabs. There was a tradition in Persia of importing knowledge from all over the world. It was based on a philosophy which regarded knowledge itself as virtue, like the Socratic philosophy. So, to make people virtuous you gather knowledge from all corners of the world. It was begun by Khusrow Noshirvan in the 6th century. At that time Justinian closed all the schools of philosophy in the Roman empire and many philosophers took refuge in the court of Noshirvan. According to the Shahnama [of Firdausi] his wazir came to India and took chess, Panchatantra etc. back to Persia. There was also an astronomical tradition in Jundishapur (Gundeshapur) in Persia. This astronomy also traveled from India. Which is interesting, because Khusrow’s court already had the most knowledgeable people in the Roman empire and if the Almagest (Almagest is the Latin form of the Arabic name al-kitabu-l-mijisti, (The Great Book) of a mathematical and astronomical treatise proposing the complex motions of the stars and planetary paths, originally written in Greek by Ptolemy of Alexandria, Egypt, written in the 2nd century. The Almagest is the most important source of information on ancient Greek astronomy-Ed) or any other advanced astronomical text existed at that time then it would have been similarly collected and translated, but we do not hear about it. On the contrary, the Almagest itself starts off by addressing an unknown “Cyrus”. So it was probably constructed in Persia. Certainly, Greek knowledge was translated into Persian and later into Arabic. But, so far as astronomy is concerned we know that the very fact that first it went [from India] to Persia and then Baghdad shows that Greek knowledge at that point did not compare in any way with the present-day versions of Ptolemy’s Almagest. There was also a strong tradition of neo-Platonism which came through texts in Greek language [though probably it originated in Egypt]. This was called the “theology of Aristotle”, and that was the primary extent of “Greek” knowledge at that time. There was no Greek knowledge available from Byzantium at that time since all the schools of philosophy there had been closed. [We also know that Arabic knowledge travelled in the other direction, to Greek texts.] The proof is that Panchatantra is translated from Sanskrit to Pahlavi (and you find its reference in Firdausi’s Shahnama) and from Pahlavi it was translated into Arabic and then from Arabic to Greek. Among the Arabs it became the basis of a movement –Ikhwan as- Safa (the Brethren of Purity); so we know the route that knowledge took from India to Greek texts, and it also traveled directly [as in Ashoka’s time when Indian texts and medicinal plants went to Alexandria]. The process really took off with Bayt al hikma (The House of Wisdom at Baghdad) which was linked to Islamic rational theology which valued knowledge as a virtue. It was closely related to aql-i-kalaam, which meant Allah has given you aql and one must apply that aql in order to interpret the Koran.
SK: Which were the sources from which knowledge was gathered in Persia?
Raju: India was one of them. I already talked about Panchatantra, medicine. Indian mathematical texts traveled to Baghdad and they were translated by Al Khwarizmi. [Because of this movement to gather knowledge in Baghdad] the demand for books increased so much that paper technology came in from China into Baghdad. We also hear in some accounts that things came from what are called Greeks [but were from Alexandria in the African continent].
SK: Was there any exchange between Persia and Greece and Persia and India during Alexander’s (Sikander) travel through Persia up to India?
Raju: There is an account in the Zoroastrian book of Nativity that Alexander got his books from the Persian emperor and got them translated. The question is: what happened to them? Presumably, some of them [the looted books] went to Aristotle [Alexander’s teacher] and some of them went to the corpus of the library of Alexandria. Aristotle was supposed to be the first person in Greece to have a library so where did his books come from?
SK: That does not sound very different from Elgin’s marbles!
Raju: (Laughs) Yes. People have not talked about the sources of books for the library of Alexandria. It could not have been those small city states in Greece, which did not have the capacity to produce them. If you look at the trial of Socrates, there were supposed to be 600-odd jurors. If you take ten persons in the population for every citizen then there would still be only about 5-6000 people in Athens so how could they produce the books on the scale of the library of Alexandria—half a million books as is normally mentioned? Only a Persia or an Egypt could have done that.
In the case of Alexander, as with other military conquerors, knowledge flows towards them in the case of barbarian incursions.
SK: Such a large collection of books in those days must have been accumulated over a long time and must have preceded Alexander also.
Raju: Exactly! It must have taken a very, very long time. Papyrus was very expensive [so it also took a lot of resources].
SK: I said this because when I was in Deccan College, Pune, I found that they are putting together a Sanskrit dictionary and after eight volumes they are still in ‘a’since they are adding on contextual meaning as a word occurs in different canonical Sanskrit texts. They have chosen 1500 classical Sanskrit works to do so, which include natya shastra, vastu shastra, ayurveda, literary and philosophical texts and so on. If they are considering 1500 as fairly representative of canonical Sanskrit texts then to have hundreds of thousands of works it must have taken many centuries and many civilisational sources.
Raju: Exactly and that is the how the real corpus of books in the Library of Alexandria accumulated. In fact, how many Greek texts can we count? Nowhere in that neighborhood! There is no possibility that those small [Greek] states could have produced that kind of knowledge. So this entire myth making about Greeks has used this library of Alexandria. Possibly there were some texts in it that came from Greece, but nowhere in the range of half a million.
SK: There must have been Mediterranean exchanges..
Raju: The exchanges between Greece and Egypt were already taking place. Greek people like Plato, Herodotus [routinely] used to come to Egypt for higher studies. Greeks were copying Egyptian gods. Each Greek god has a counterpart in Egypt and in fact Herodotus says that explicitly.
SK: After all Egypt was a much older civilization by a couple of millennia. Did this exchange continue after the Baghdad period also?
Raju: Yes this culture of libraries spread in the entire Islamic world even in Cordoba, Spain during the Islamic period. Al Beruni when he came to India made it a point to collect knowledge of all kinds. The Baghdad book bazaar had become prominent, and this [tradition] persisted [in Islam] at least till the 12th -13th century.
SK: Arabs have been depicted as carriers and safe keepers of knowledge rather than creators of knowledge. Can you comments on that.
Raju: There is an enormous amount of evidence to the contrary. [The book mentions the case of Copernicus, where the Arabs were clearly the creators and the Europeans merely the carriers of knowledge. So] it is good to look at the question: how did this story start? (that Arabs were mere safe keepers of Greek knowledge).
SK: In fact they have been depicted as barbaric nomads killing each other, who did not have any culture till the British formed various nation states in Arabia. Thus there were Pharaohs and then there were Bedouins till the Anglo-Saxons came…
Raju: If you look at Arab literature (pre-Islamic) there is a depiction of a freewheeling society living in the desert. Post Islam, they conquered Persia and absorbed a lot of administrative structure of the Persians and then there was this culture of books and libraries. That itself shows that they had to produce books. It is a different matter that in a bazaar to get a higher price one might say not me but somebody more famous wrote this, or it was written a long time back and make it an antique etc. After all, a lot of things happen in a market. It is undeniable that Arabs were creative and made contributions so one should look at when did the story start that Arabs are only safe keepers. It started during the Crusades. They [the Christians of Europe] were fighting a religious war and Europe had a tradition of book burning. In fact, there were many fiats [by Christian emperors] right from 4th century to burn books. The library of Alexandria was burnt down. There was a tradition of burning heretical books which included secular knowledge. Within Christendom, there was not much of a culture of books and when they were fighting the Arabs they realized that they needed secular knowledge which was available in books. They captured Toledo which had a massive library [coming from] the Umayyad khilafat. It took a lot of time [for the church] to arrive at the decision to translate those books [and not burn them]. This needed a justification. That was concocted by saying that this knowledge belongs to Greece and the Greeks were theologically ‘correct’. This was regarding early Greeks mind you, since they were pre-Christian, whereas they [the church] had conflicts with later Greeks like Proclus, Theon etc. The advantage of inventing a person like Euclid was that you can attribute a philosophy to that individual which suits you.
SK: Is there any Church document or correspondence which discusses these things?
Raju: The church does not operate like that. They are not accessible. Even what the Church did in India is not accessible. If I wish to know what happened in India during the Inquisition then I don’t get access to that even if the records exist. It is not an open archive. I would rather not demand documentary evidence. In this entire [church] tradition, so many documents have been cooked up or forged. After all, even in Delhi, periodically fires go on in so many ministries and documents get burnt (laughs). Let us look at common sense and circumstantial evidence.
SK: What do you consider as Greek contributions, you have raised some questions about their arithmetical capabilities…
Raju: It is clear from their system that it was completely inadequate to do quick sums; forget about subtractions and divisions. I don’t know what their contributions were in science. I don’t have any evidence of that. May be in theatre or other things, however there is strong evidence that some ideas including Platonic ideas come from the mystery geometry tradition of Egypt.
SK: What is mystery geometry?
Raju: I have written a new book on Euclid and the mystery geometry of Egypt. If you see how Plato looks at geometry. He says it should be taught to students in his Republic, which is an ideal state. He has written about how its citizens should be trained—he particularly talks about two subjects viz music and mathematics—in order for their souls to be virtuous. The very word mathematics comes from mathesis, which means learning. What is learning? Socrates demonstrates it by calling a slave boy and asking him questions, thereby showing that the slave boy has an intrinsic knowledge of geometry. He says this is possible because the boy has a soul and the soul is recollecting the knowledge from the previous birth. In fact, the Platonic doctrine is that “all learning is recollection”. Mathematical truths are eternal, and since the soul is eternal, by sympathetic magic they [the eternal truths] arouse the soul. Thus the function of mathematics is to arouse the soul through introspection, by taking you away from the external world. This is the idea of mystery geometry. The practical applications are of no concern to us says Plato, the moral applications are more important.
SK: There are these well known names of Pythagoras and later Archimedes..
Raju: Pythagoras is a school which indulged in mystery mathematics of numbers etc. There is an exoteric part which is told to outsiders and there an esoteric part which is told to initiates. What is the evidence of Pythagoras and the proof of his theorem? [Deductive] proof is a concept post-12th century. At that time [in Pythagoras’ time] it [geometry] was only for arousing the soul. In the mystery tradition the soul knows what truth is and that [intrinsic knowledge of the soul] is the ultimate standard [of truth]. That belief about the soul came into violent conflict with [post-Nicene] Christianity, even though that notion of soul was very much part of early Christianity of Origen. From his notes the present day Bible is derived. He was declared a heretic. The doctrine of love was entirely a mystery tradition. But, after the Church and State came together in the 4th century you could not say that everyone would be saved. There had to be some advantage in becoming a Christian. It is like the state saying I am going to treat my citizens above those of other states. It brings in a boundary: this is ours and that is theirs. That is why Proclus was declared a heretic. Because he said mathematics deals with eternal truths, since the soul is eternal, therefore the cosmos should also be eternal. That goes against the [church] doctrine: for then there will be no creation and no apocalypse, so he was declared a heretic. So was the case of Hypatia and her father Theon (both prominent mathematicians from Alexandria—Ed). Clearly Christianity was uncomfortable with this interpretation of Elements and looked at it as heretical. Then Thomas Aquinas (1225-1274) reinterpreted Elements and used it as a weapon against Islam. Basically at that point in time Christendom had realized that it was not possible to spread beyond Spain by force alone. Moreover Europe was still very poor compared to the Arabs and they still coveted that money [the Arabs had]. Even though it [the Crusades] was called a religious war, it was motivated by material concerns. Like the Iraq war, which is not based on moral concerns, but on the oil wealth in the region.
Since it could not be done by warfare the church realized that it also had to adopt the method of argumentation and discourse. Quoting the [Christian] scriptures would not work with the Arabs. Thus, a third ground had to be found. That was found in the neo-Platonism that had already fascinated Islam in the form of aql-i-kalaam or falsafaa. Therefore, Aquinas realized that reason was needed to influence the Arabs. Thus, after Augustine, there was a second period of change in the Christian theological doctrine in the post-Crusade era. It was called Christian rational theology and was an adaptation of Islamic rational theology. This tried to establish universal principles of ‘proof’ [to persuade the Islamic Arabs]. That is where Elements came in.
SK: But did this not create a dichotomy within Christianity, how do you reconcile faith with reason?
Raju: It did indeed. Initially a whole lot of books ascribed to Aristotle, were banned and placed on the Index, since they were thought to be contrary to the doctrines of the Church. But then there was a whole army of people working on it who were trying to reconcile these contradictory beliefs. So it took time for “Aristotle” to be accepted into the [Christian] system. There was a process of absorption via reinterpretation. Thus Elements was reinterpreted from the tradition of mystery geometry to something which gives you a universal ‘proof’.
SK: It is like Vedanta, which says everyone is a part of the Brahman, at the same time it coexisted with the caste system…
Raju: Yes, for example there is this famous story of Shankaracharya and the chandaal, where he prostrates himself in front of the chandaal, but later it is reinterpreted. It is said that chandaal was actually a reincarnation of Shiva etc..
SK: One of the important theses put forward by you is that mathematics has cultural foundations. Can you say that there is an Indian way of doing mathematics if so what are its features?
Raju: There are some clear cut features. In India there was just one notion of proof of praman which was applied everywhere: be it philosophy, mathematics or physics. The first praman was pratyaksh. Empirical means were accepted as proof. This you find in sulbasutras, in Aryabhata, and right down to Yuktibhasha. For example the so called ‘Pythagorean theorem’ could be proved by drawing the triangle on a palm leaf, and it could be shown that the square on the ‘diagonal’ was equal to the sum of the squares on the other two sides. This could be shown by cutting, rotating etc. Whereas the European tradition would disagree and say that mathematics is purely metaphysical and by bringing in motion you are bringing in physics and it violates the basic idea of geometry as concerned with immovable space. That is one major source of tension. [Secondly], today the notion of proof is seen in a very rigid manner in a completely metaphysical way. How do you carry out deduction? on what logical basis? This is unclear in the Indian tradition. After all there are different systems of logic which are prevalent. There is the Jain system of syadvad and saptabhangi, there is Buddhist logic of chatuskoti and so on. In fact, in the debates between Naiyayikas and Buddhists over a thousand year period you find that they are not addressing each other’s issues because of differing concepts of anumaan [or deduction]. But Europeans declare their logic as universal, when it is not. There is a third aspect which I have called zeroism, which has to do with what is mathematics good for. In the neo-Platonic view it is good for the soul. The European view is that mathematics is good for providing proof. But in India, the aim of mathematics was not to provide praman but to do something vyavaharik, something practical, which is removed from soul etc. If I am doing something vyavaharik, I don’t mind making approximations. If I am computing, then the computer is going to make so many approximations. Many things are discarded or zeroed, and that is acceptable. However European mathematics demands perfection where you cannot discard the smallest entity. The belief in perfection comes from a religious view of mathematics. It then gets into theology that God made the world and he wrote the laws in the language of mathematics [which must hence be perfect]. In India it is calculations.
SK: The word for mathematics in India is ganit that is counting..
Raju: Yes it is numerical calculation. There are proofs and they can be empirical and one particular logic is not considered universal. [So proofs are not the focal concern.]
SK: When pratyaksh praman is not available you bring in inference etc. Clearly mathematics was considered something physical. Can you explain the concept of universalism that is prevalent in mathematics.
Raju: Universality is factually incorrect. The way mathematics was done in India was different from Europe. So the Indian place value system and algorithms or calculus took such a long time to be absorbed by the Europeans. Metaphysics is never universal. The moment mathematical proof becomes metaphysical it ceases to be universal. In fact it can become ‘universal’ only to the extent that it is demonstrable empirically (pratyaksh). Universality is just a European prejudice as they are ill informed about other cultures, so they declare universality from a parochial point of view.
SK: The crude way in which universality is put forward is by saying that 2+2=4, no matter where you are in Greece or Arabia, India or China…
Raju: It is not true, and I have argued it at great length in my paper presented in Hawaii. Let us say we are using a computer to add. 2+2 is a complicated case, so let us take 1+1, The answer could be 1 or even 0 depending on what kind of logic gate one is using. So, I have to specify and say I am using integers. But what are integers? If I do arithmetic with integers on computers say using a C program on a 16 bit machine it will not give 2 as the answer but something else unless I do rounding off. In order to specify what are integers I need infinite time and infinite memory. In a commercial transaction we get into an agreement saying Rs 2 plus Rs 2 would be Rs 4. But that is an agreement. It is not a universal truth. If I have two stones and if I take up two more stones then I get four stones but if I break one of them into two then I get five stone pieces. So I have to be careful about them as universal truths. At a practical level there is no problem. Even if there is no formal agreement or legal frame work, I would simply say you broke the stone. An agreement is not a universal truth or ultimate truth etc.
SK: The statement that numbers are metaphysical transcendental, entities is itself a metaphysical statement.
Raju: That is exactly the point. So long as you are in the domain of convenience it is fine. If you look at Indian texts they will have numbers with 18 digits. What will you do if you need more? you go to 20, 30 or 40 places for a particular purpose. Normally you don’t need more than 18 places. Yajurved goes only till 12 places. Aryabhat goes to 18 places. It is a matter of convenience, but you never go to an infinity of places. That is also how computer arithmetic is done. You round off after some time, and that is perfectly fine but then don’t talk about universal truth.
There is an example given in ethno-mathematics. Suppose I have borrowed two fish from you and I have returned two fish. It won’t do if I have borrowed two big fish and then returned two tiny fish. There is a sense of exchange and fairness involved, not universal truth.
SK: What is the European view on standard of proof etc.
Raju: There is the Platonic deprecation of the empirical. Then there is the clerical elevation of metaphysics over the empirical. The clergy said the metaphysical is a higher truth than the empirical truth. That is fallacious. Metaphysics is decided by a coterie.
What Hilbert did is that he analysed the Elements from this perspective: for example, the proposition 1.4 [of the Elements] or the SAS [Side-Angle-Side] theorem involves physical movement in space, like the Yuktibhasha proof of the “Pythagorean Theorem”. They said the empirical has got into mathematics, which [empirical] is perishable, not eternal, it involves motion hence physics, whereas geometry should be concerned only with properties of immovable space and so on.
So Hilbert said if this theorem is made a postulate then everything becomes metaphysical. Thus he removed the last vestiges of empirical elements in the ‘Elements’. Or at least he thought he did. But actually he could not because he had this notion of congruence which fails after proposition 1.35, the one which is used to derive the area of a triangle. There [in 1.35] congruence is not in the sense of being of the same shape but same area. Earlier propositions are about congruent triangles where you [may] just transfer attention from one shape to the other without moving them. Now [in 1.35] they are incongruent but they are equal in area. The word used in Elements is not “congruent” but “equal”. Equal again is related to equality of the soul as in say Advaita Vedanta which is also a political statement of equality of all people who might look dissimilar. The esoteric meaning is equality of dissimilar things. The way out taken by Hilbert is to define area. But how do you define area without defining length? But if you do define length then the entire Elements becomes trivial as Birkhoff showed with the metric. Thus by throwing out the empirical you start introducing peculiar and artificial things [like defining area without allowing length to be defined] Thus, Hilbert made mathematics completely metaphysical through his ‘axiomatic’ approach.
Now a lot of proofs in mathematics are based on reductio ad absurdum, which depends on two valued logic which would not be acceptable in the Indian tradition at all. So how are these proofs universal?
It is all based on and tightly tied to the [historical] perception that Aristotle the Greek did some logic etc. Of course, one does not even consider that what is called “Aristotelian logic” [might] actually have come from Naiyaikas, through the Arabs. It is a misnomer to call it “Aristotelian”. In my article on Logic for the Springer Encyclopedia of Non-Western Science, Technology, and Medicine, I have made this point that the Aristotelian syllogism is [historically] not to be found anywhere [in Greece]! There is a Stoic syllogism [in Alexandria], but then these things [Aristotelian syllogism] suddenly appear in Toledo and that is problematic.
SK: But syllogism is a very prominent part of Nyaya..
Raju: Yes that is the point, and we also know that Nyaya went to Baghdad. Anyway, the standard approach in mathematics is not universal but has been universalized. First there was the ignorance of Europeans and this ignorance has been universalized through the process of colonization. On the one side [in Americas] people are just killed off, and on the other side they are given Western education where they were given a fabricated history which made them feel inferior. The Indian elite in the 19th century swallowed this and found the solution in aping the west. This has persisted even after independence. My demand is Swaraj in science and in science education.
SK: The creative process is not deductive, otherwise rule-based machines could have done it. But post-facto deduction may be used to teach. However if again our students at the frontiers of research are not going to use the deductive approach then what is the use of even teaching this method?
Raju: Why is mathematics difficult? My answer to that is that math per se is not difficult. But if you look at the text of NCERT for 12th standard, and particularly in Hindi, you find terms like continuity, differentiability, formal real numbers, set theory etc. All this is extremely difficult to follow [in Hindi] even though I have studied all that. It is so terribly convoluted. Where are their primary axioms? They are in set theory, which enables me to axiomatically perform infinite processes, which I cannot ever hope to perform. With the axiom of choice I can have a choice function, I can claim its “existence” etc. It is only through such metaphysical and imaginary infinite processes that one can preserve the perfection of mathematics required by Western theology.
Apart from all these theological principles that have come in, you cannot teach set theory for 10th standard students, so you cannot teach the axiomatic deductive process today. I can do that only at the MSc level and very few people come to that level. The vast majority hence cannot be taught mathematics. You have to tell them a set is a collection of objects! A student has to be taught what is a ring and a field. What utter nonsense! It is very bad pedagogy.
SK: I see a great danger in this. The common perception is that Indians are good in mathematics and good with numbers. That comes from a different tradition than this abstract set theoretic one. By adopting this in our schools we are subverting ourselves!
Raju: That is right and that is the point I have made to the Knowledge Commission. Our culture has some good points and by dropping them we are subverting ourselves.
SK: A very senior executive the chairman of a large bank in Japan told me “We Japanese cannot do software because it is abstract we can do manufacturing very well. We can make things cheaper, faster, smaller etc but not deal with abstractions. Whereas Indian can do it well because they have a philosophic tradition which we lack.” I ventured to say “but you have Zen” and he just brushed it aside.
Raju: That is interesting. I hope it is true. But we are actually adopting counter cultural traditions. There is no discussion of all these things in the public space. I would like to build a quantum computer based on Buddhist logic of chatuskoti, but where is the space to discuss this?
We need to discuss what we need to teach. Somebody just sits behind closed doors and decides what should be taught and that is not correct. There is no reason. Just that we should continue to ape the west. This is how things are made ‘universal’ by a class which is educated in the western tradition and are treated as experts. If experts cannot engage in critical thinking then how do you expect the students to do it?
It is not possible to do computer arithmetic without discarding some part of a number. As soon as we start looking at what a floating point number is, we find that it is not part of a ring or a field or anything! The basic so called associative law is not obeyed. By the way, whose law? why “law”? These are all theological concepts, that the numbers must obey the law etc. All the standard algebraic structures are useless [for computer arithmetic].
In reality, there is a practical way of doing things which is embodied in the way these data types like floating point numbers are used, which is different from theoretical computer science. This encompasses a different philosophy which is closer to what I am talking about. I am talking about practical computation, where we can discard these things. But on what logic? not based on perfection or universalism! You tell me how many decimal places you need and I can procure them. That is where shoonyavad or zeroism comes in. Based on this zeroism I am conducting a course on “Calculus without Limits” in Central University of Tibetan Studies in Sarnath. I am demonstrating it to show how much simpler life can be without universalism or set theory etc.
If we say we are a secular state why should we bring in theology in mathematics, after all if I use Buddhist logic many of the theorems in mathematics will fail! We should teach secular and practical mathematics. We are doing it because the universities in the west are doing it. But those universities were erected for theological purposes. According to [Isaac] Barrow, Cambridge University was established to breed clerics!
SK: I think seeing the pragmatism embedded in western societies today I think if you build a quantum computer using Buddhist logic that can threaten the encryption involved US financial system then you would have proved your point and billions of dollars will be spent on research on alternative logic.
Raju: That is accepted. We do need to find applications, but for me the very fact that people will be able to understand much of mathematics using this new system itself would be a worth it. I don’t care if the west wants to do it or not. My son should be able to do calculations easily which he could not do earlier.
SK: I will give an example to illustrate what I was saying. Fuzzy Logic was invented by Lotfi Zadeh, a Iranian professor at University of Berkeley. There were people who called it cocaine of mathematics implying that he was high on drugs and invented this since it did not follow the normal Aristotelian binary logic. The Japanese picked it up and used it in all appliances like washing machines, TV etc. The Americans picked it up only in the 80s because they had launched an armed commando raid on Tehran in 78-79 during the hostage crisis. But the control systems of their military helicopters carrying the commandos could not stand the heat and dust of the desert. They crashed and the mission was a failure. Then they realized they needed fuzzy logic based adaptive control systems and they brought them in. In that sense they are not theological.
Raju: My concern is not to convert the west. My concern is if these theological concepts have crept into mathematics then that mathematics should NOT be taught in this country. We should teach secular mathematics. After all it is being used to condition people, inculcate inferiority in them through fake history etc.
SK: It is definitely driving people away from mathematics.
Raju: And these kids keep looking at pictures of a fake Euclid and a fake Pythagoras as white Caucasians which we see in text books, and grow up in awe of the west and say the solution to any problem is to ape the west. If we can break out of those things that itself would be an achievement.
SK: One last comment. Many have objections to the way the Indian mathematical results are written in the form of a sutra without explaining how they arrived at it or what is the justification for it. Is there any insight into how they achieved these results? Secondly, one person who wrote many results filling up many note books without giving proof is Srinivasan Ramanujan though it was in the field of analysis in the western tradition.
Raju: I am not arguing for an absence of process. To deny the value of deductive proof is one thing, and to say that there should be complete absence of process is another thing. I would assert that though there was the sutra tradition there were also Yuktibhasa, Yukti Deepika etc where they explain the process, perhaps due to Jesuit pressure! They were written after the arrival of Europeans in Cochin. A sutra has to be terse to make it easy to remember. It is a cultural matter [in the oral tradition] that here we are dealing with minds of human beings and hence the communication should be from one mind to another and not filtered through a derivation on a dead parchment where it is liable to be misunderstood. Right or wrong that seemed to have been the cultural tradition and an oral tradition. After all even Vedas are not written down. That is not a critical issue dealing with validity but a pedagogical matter.
Certainly a process has to be there and a justification [praman] has to be there. In my book [Cultural Foundations of Mathematics] I have shown [in Chapter 3] that there is complete praman for the infinite series in India, but the derivation is on different philosophical principles. I don’t say that first I should have set theory which allows me to do some infinite processes and then I should have an infinite set of numbers and then prove convergence and so on. That is the rigmarole of Western mathematics.
I want to sum the series and the stated criterion is that the sum should remain constant when I add two consecutive terms. How does it remain constant? Up to the level of accuracy and the decimal (or sexagesimal) places I need. This is similar to epsilon-delta [and the “Cauchy” criterion] but deals with a finite number of terms [and does not involve a infinite metaphysical process]. That is a perfectly good criterion.
SK: That is what physicists do when they sum any series like Raleigh-Schroedinger perturbation series. You calculate to the second order of approximation and if there is serious problem you go to the next order.
Raju: That is how all computer algorithms are done. It only ceases to be valid if you demand perfection! That is a perfectly practical attitude. It is not that process and proof are missing. It is just proof from a different philosophical position.
The first text book on philosophy that I picked up from my father said, there is no philosophical tradition in India but only poetry! For philosophy you have to read the Greeks! So now I can say that there is no mathematical tradition in Europe and it is all theology which was imported here through colonialism!
What happened with Elements is that it had come to India through Islam but it was not translated into Sanskrit till very late at the time of Sawai Jai Singh in 1723, long after the arrival of Jesuits in Jehangir’s court. There were two parallel distinct traditions. Akbar’s courtier (Abul Fazl) who wrote the Ain-e-Akbari talks about learning from the Elements. It was there in Arabic and Persian traditions but was not considered valuable by Indian mathematicians. It was considered something religious. Also, practically Pythagoras theorem comes at the end of the Elements where as Yuktibhasa starts with it, with a different way of proving it without the forty odd earlier results.
So I would say it is a religious belief which is being universalized and I find it highly objectionable. I would say, in fact, our principles are universal since they are empirical and physical. I would characterize present-day mathematics as European ethno-mathematics tainted by theology.
Ghadar Jari Hai—The Revolt Continues, Vol III, No. 3&4, July-Dec, 2009
Peepul ke Neeche
“Indian mathematics is practical whereas the European is metaphysical”
C K Raju has been arguing passionately through several lectures and books about the uniqueness of ancient Indian mathematics and how it influenced the rest of the world. He says what is taught as standard modern mathematics today, is based on theological positions taken by the Church after the Crusades. Shivanand Kanavi conversed with Raju on the results of his research in the history and philosophy of mathematics.
Shivanand: Dr Raju welcome to peepul ke neeche conversation. Having looked at some of your writings, I see that you have researched deeply into the mathematical tradition of India as well as that of Persia, Arabia and Europe. Could you give us an overview of exchanges between India and West Asia in the field of mathematics?
Raju: As I have stated in the book (Is Science Western in Origin?—C K Raju), the process of exchange with Arabs started with Barmakids (barmak from pramukh, Persian-Buddhists who were wazirs to Abbasid Khalifas--Ed), this was around 8th century CE, after the conquest of Persia by the Arabs. Besides the spread of Islam in Persia, Persian customs spread to the Arabs. There was a tradition in Persia of importing knowledge from all over the world. It was based on a philosophy which regarded knowledge itself as virtue, like the Socratic philosophy. So, to make people virtuous you gather knowledge from all corners of the world. It was begun by Khusrow Noshirvan in the 6th century. At that time Justinian closed all the schools of philosophy in the Roman empire and many philosophers took refuge in the court of Noshirvan. According to the Shahnama [of Firdausi] his wazir came to India and took chess, Panchatantra etc. back to Persia. There was also an astronomical tradition in Jundishapur (Gundeshapur) in Persia. This astronomy also traveled from India. Which is interesting, because Khusrow’s court already had the most knowledgeable people in the Roman empire and if the Almagest (Almagest is the Latin form of the Arabic name al-kitabu-l-mijisti, (The Great Book) of a mathematical and astronomical treatise proposing the complex motions of the stars and planetary paths, originally written in Greek by Ptolemy of Alexandria, Egypt, written in the 2nd century. The Almagest is the most important source of information on ancient Greek astronomy-Ed) or any other advanced astronomical text existed at that time then it would have been similarly collected and translated, but we do not hear about it. On the contrary, the Almagest itself starts off by addressing an unknown “Cyrus”. So it was probably constructed in Persia. Certainly, Greek knowledge was translated into Persian and later into Arabic. But, so far as astronomy is concerned we know that the very fact that first it went [from India] to Persia and then Baghdad shows that Greek knowledge at that point did not compare in any way with the present-day versions of Ptolemy’s Almagest. There was also a strong tradition of neo-Platonism which came through texts in Greek language [though probably it originated in Egypt]. This was called the “theology of Aristotle”, and that was the primary extent of “Greek” knowledge at that time. There was no Greek knowledge available from Byzantium at that time since all the schools of philosophy there had been closed. [We also know that Arabic knowledge travelled in the other direction, to Greek texts.] The proof is that Panchatantra is translated from Sanskrit to Pahlavi (and you find its reference in Firdausi’s Shahnama) and from Pahlavi it was translated into Arabic and then from Arabic to Greek. Among the Arabs it became the basis of a movement –Ikhwan as- Safa (the Brethren of Purity); so we know the route that knowledge took from India to Greek texts, and it also traveled directly [as in Ashoka’s time when Indian texts and medicinal plants went to Alexandria]. The process really took off with Bayt al hikma (The House of Wisdom at Baghdad) which was linked to Islamic rational theology which valued knowledge as a virtue. It was closely related to aql-i-kalaam, which meant Allah has given you aql and one must apply that aql in order to interpret the Koran.
SK: Which were the sources from which knowledge was gathered in Persia?
Raju: India was one of them. I already talked about Panchatantra, medicine. Indian mathematical texts traveled to Baghdad and they were translated by Al Khwarizmi. [Because of this movement to gather knowledge in Baghdad] the demand for books increased so much that paper technology came in from China into Baghdad. We also hear in some accounts that things came from what are called Greeks [but were from Alexandria in the African continent].
SK: Was there any exchange between Persia and Greece and Persia and India during Alexander’s (Sikander) travel through Persia up to India?
Raju: There is an account in the Zoroastrian book of Nativity that Alexander got his books from the Persian emperor and got them translated. The question is: what happened to them? Presumably, some of them [the looted books] went to Aristotle [Alexander’s teacher] and some of them went to the corpus of the library of Alexandria. Aristotle was supposed to be the first person in Greece to have a library so where did his books come from?
SK: That does not sound very different from Elgin’s marbles!
Raju: (Laughs) Yes. People have not talked about the sources of books for the library of Alexandria. It could not have been those small city states in Greece, which did not have the capacity to produce them. If you look at the trial of Socrates, there were supposed to be 600-odd jurors. If you take ten persons in the population for every citizen then there would still be only about 5-6000 people in Athens so how could they produce the books on the scale of the library of Alexandria—half a million books as is normally mentioned? Only a Persia or an Egypt could have done that.
In the case of Alexander, as with other military conquerors, knowledge flows towards them in the case of barbarian incursions.
SK: Such a large collection of books in those days must have been accumulated over a long time and must have preceded Alexander also.
Raju: Exactly! It must have taken a very, very long time. Papyrus was very expensive [so it also took a lot of resources].
SK: I said this because when I was in Deccan College, Pune, I found that they are putting together a Sanskrit dictionary and after eight volumes they are still in ‘a’since they are adding on contextual meaning as a word occurs in different canonical Sanskrit texts. They have chosen 1500 classical Sanskrit works to do so, which include natya shastra, vastu shastra, ayurveda, literary and philosophical texts and so on. If they are considering 1500 as fairly representative of canonical Sanskrit texts then to have hundreds of thousands of works it must have taken many centuries and many civilisational sources.
Raju: Exactly and that is the how the real corpus of books in the Library of Alexandria accumulated. In fact, how many Greek texts can we count? Nowhere in that neighborhood! There is no possibility that those small [Greek] states could have produced that kind of knowledge. So this entire myth making about Greeks has used this library of Alexandria. Possibly there were some texts in it that came from Greece, but nowhere in the range of half a million.
SK: There must have been Mediterranean exchanges..
Raju: The exchanges between Greece and Egypt were already taking place. Greek people like Plato, Herodotus [routinely] used to come to Egypt for higher studies. Greeks were copying Egyptian gods. Each Greek god has a counterpart in Egypt and in fact Herodotus says that explicitly.
SK: After all Egypt was a much older civilization by a couple of millennia. Did this exchange continue after the Baghdad period also?
Raju: Yes this culture of libraries spread in the entire Islamic world even in Cordoba, Spain during the Islamic period. Al Beruni when he came to India made it a point to collect knowledge of all kinds. The Baghdad book bazaar had become prominent, and this [tradition] persisted [in Islam] at least till the 12th -13th century.
SK: Arabs have been depicted as carriers and safe keepers of knowledge rather than creators of knowledge. Can you comments on that.
Raju: There is an enormous amount of evidence to the contrary. [The book mentions the case of Copernicus, where the Arabs were clearly the creators and the Europeans merely the carriers of knowledge. So] it is good to look at the question: how did this story start? (that Arabs were mere safe keepers of Greek knowledge).
SK: In fact they have been depicted as barbaric nomads killing each other, who did not have any culture till the British formed various nation states in Arabia. Thus there were Pharaohs and then there were Bedouins till the Anglo-Saxons came…
Raju: If you look at Arab literature (pre-Islamic) there is a depiction of a freewheeling society living in the desert. Post Islam, they conquered Persia and absorbed a lot of administrative structure of the Persians and then there was this culture of books and libraries. That itself shows that they had to produce books. It is a different matter that in a bazaar to get a higher price one might say not me but somebody more famous wrote this, or it was written a long time back and make it an antique etc. After all, a lot of things happen in a market. It is undeniable that Arabs were creative and made contributions so one should look at when did the story start that Arabs are only safe keepers. It started during the Crusades. They [the Christians of Europe] were fighting a religious war and Europe had a tradition of book burning. In fact, there were many fiats [by Christian emperors] right from 4th century to burn books. The library of Alexandria was burnt down. There was a tradition of burning heretical books which included secular knowledge. Within Christendom, there was not much of a culture of books and when they were fighting the Arabs they realized that they needed secular knowledge which was available in books. They captured Toledo which had a massive library [coming from] the Umayyad khilafat. It took a lot of time [for the church] to arrive at the decision to translate those books [and not burn them]. This needed a justification. That was concocted by saying that this knowledge belongs to Greece and the Greeks were theologically ‘correct’. This was regarding early Greeks mind you, since they were pre-Christian, whereas they [the church] had conflicts with later Greeks like Proclus, Theon etc. The advantage of inventing a person like Euclid was that you can attribute a philosophy to that individual which suits you.
SK: Is there any Church document or correspondence which discusses these things?
Raju: The church does not operate like that. They are not accessible. Even what the Church did in India is not accessible. If I wish to know what happened in India during the Inquisition then I don’t get access to that even if the records exist. It is not an open archive. I would rather not demand documentary evidence. In this entire [church] tradition, so many documents have been cooked up or forged. After all, even in Delhi, periodically fires go on in so many ministries and documents get burnt (laughs). Let us look at common sense and circumstantial evidence.
SK: What do you consider as Greek contributions, you have raised some questions about their arithmetical capabilities…
Raju: It is clear from their system that it was completely inadequate to do quick sums; forget about subtractions and divisions. I don’t know what their contributions were in science. I don’t have any evidence of that. May be in theatre or other things, however there is strong evidence that some ideas including Platonic ideas come from the mystery geometry tradition of Egypt.
SK: What is mystery geometry?
Raju: I have written a new book on Euclid and the mystery geometry of Egypt. If you see how Plato looks at geometry. He says it should be taught to students in his Republic, which is an ideal state. He has written about how its citizens should be trained—he particularly talks about two subjects viz music and mathematics—in order for their souls to be virtuous. The very word mathematics comes from mathesis, which means learning. What is learning? Socrates demonstrates it by calling a slave boy and asking him questions, thereby showing that the slave boy has an intrinsic knowledge of geometry. He says this is possible because the boy has a soul and the soul is recollecting the knowledge from the previous birth. In fact, the Platonic doctrine is that “all learning is recollection”. Mathematical truths are eternal, and since the soul is eternal, by sympathetic magic they [the eternal truths] arouse the soul. Thus the function of mathematics is to arouse the soul through introspection, by taking you away from the external world. This is the idea of mystery geometry. The practical applications are of no concern to us says Plato, the moral applications are more important.
SK: There are these well known names of Pythagoras and later Archimedes..
Raju: Pythagoras is a school which indulged in mystery mathematics of numbers etc. There is an exoteric part which is told to outsiders and there an esoteric part which is told to initiates. What is the evidence of Pythagoras and the proof of his theorem? [Deductive] proof is a concept post-12th century. At that time [in Pythagoras’ time] it [geometry] was only for arousing the soul. In the mystery tradition the soul knows what truth is and that [intrinsic knowledge of the soul] is the ultimate standard [of truth]. That belief about the soul came into violent conflict with [post-Nicene] Christianity, even though that notion of soul was very much part of early Christianity of Origen. From his notes the present day Bible is derived. He was declared a heretic. The doctrine of love was entirely a mystery tradition. But, after the Church and State came together in the 4th century you could not say that everyone would be saved. There had to be some advantage in becoming a Christian. It is like the state saying I am going to treat my citizens above those of other states. It brings in a boundary: this is ours and that is theirs. That is why Proclus was declared a heretic. Because he said mathematics deals with eternal truths, since the soul is eternal, therefore the cosmos should also be eternal. That goes against the [church] doctrine: for then there will be no creation and no apocalypse, so he was declared a heretic. So was the case of Hypatia and her father Theon (both prominent mathematicians from Alexandria—Ed). Clearly Christianity was uncomfortable with this interpretation of Elements and looked at it as heretical. Then Thomas Aquinas (1225-1274) reinterpreted Elements and used it as a weapon against Islam. Basically at that point in time Christendom had realized that it was not possible to spread beyond Spain by force alone. Moreover Europe was still very poor compared to the Arabs and they still coveted that money [the Arabs had]. Even though it [the Crusades] was called a religious war, it was motivated by material concerns. Like the Iraq war, which is not based on moral concerns, but on the oil wealth in the region.
Since it could not be done by warfare the church realized that it also had to adopt the method of argumentation and discourse. Quoting the [Christian] scriptures would not work with the Arabs. Thus, a third ground had to be found. That was found in the neo-Platonism that had already fascinated Islam in the form of aql-i-kalaam or falsafaa. Therefore, Aquinas realized that reason was needed to influence the Arabs. Thus, after Augustine, there was a second period of change in the Christian theological doctrine in the post-Crusade era. It was called Christian rational theology and was an adaptation of Islamic rational theology. This tried to establish universal principles of ‘proof’ [to persuade the Islamic Arabs]. That is where Elements came in.
SK: But did this not create a dichotomy within Christianity, how do you reconcile faith with reason?
Raju: It did indeed. Initially a whole lot of books ascribed to Aristotle, were banned and placed on the Index, since they were thought to be contrary to the doctrines of the Church. But then there was a whole army of people working on it who were trying to reconcile these contradictory beliefs. So it took time for “Aristotle” to be accepted into the [Christian] system. There was a process of absorption via reinterpretation. Thus Elements was reinterpreted from the tradition of mystery geometry to something which gives you a universal ‘proof’.
SK: It is like Vedanta, which says everyone is a part of the Brahman, at the same time it coexisted with the caste system…
Raju: Yes, for example there is this famous story of Shankaracharya and the chandaal, where he prostrates himself in front of the chandaal, but later it is reinterpreted. It is said that chandaal was actually a reincarnation of Shiva etc..
SK: One of the important theses put forward by you is that mathematics has cultural foundations. Can you say that there is an Indian way of doing mathematics if so what are its features?
Raju: There are some clear cut features. In India there was just one notion of proof of praman which was applied everywhere: be it philosophy, mathematics or physics. The first praman was pratyaksh. Empirical means were accepted as proof. This you find in sulbasutras, in Aryabhata, and right down to Yuktibhasha. For example the so called ‘Pythagorean theorem’ could be proved by drawing the triangle on a palm leaf, and it could be shown that the square on the ‘diagonal’ was equal to the sum of the squares on the other two sides. This could be shown by cutting, rotating etc. Whereas the European tradition would disagree and say that mathematics is purely metaphysical and by bringing in motion you are bringing in physics and it violates the basic idea of geometry as concerned with immovable space. That is one major source of tension. [Secondly], today the notion of proof is seen in a very rigid manner in a completely metaphysical way. How do you carry out deduction? on what logical basis? This is unclear in the Indian tradition. After all there are different systems of logic which are prevalent. There is the Jain system of syadvad and saptabhangi, there is Buddhist logic of chatuskoti and so on. In fact, in the debates between Naiyayikas and Buddhists over a thousand year period you find that they are not addressing each other’s issues because of differing concepts of anumaan [or deduction]. But Europeans declare their logic as universal, when it is not. There is a third aspect which I have called zeroism, which has to do with what is mathematics good for. In the neo-Platonic view it is good for the soul. The European view is that mathematics is good for providing proof. But in India, the aim of mathematics was not to provide praman but to do something vyavaharik, something practical, which is removed from soul etc. If I am doing something vyavaharik, I don’t mind making approximations. If I am computing, then the computer is going to make so many approximations. Many things are discarded or zeroed, and that is acceptable. However European mathematics demands perfection where you cannot discard the smallest entity. The belief in perfection comes from a religious view of mathematics. It then gets into theology that God made the world and he wrote the laws in the language of mathematics [which must hence be perfect]. In India it is calculations.
SK: The word for mathematics in India is ganit that is counting..
Raju: Yes it is numerical calculation. There are proofs and they can be empirical and one particular logic is not considered universal. [So proofs are not the focal concern.]
SK: When pratyaksh praman is not available you bring in inference etc. Clearly mathematics was considered something physical. Can you explain the concept of universalism that is prevalent in mathematics.
Raju: Universality is factually incorrect. The way mathematics was done in India was different from Europe. So the Indian place value system and algorithms or calculus took such a long time to be absorbed by the Europeans. Metaphysics is never universal. The moment mathematical proof becomes metaphysical it ceases to be universal. In fact it can become ‘universal’ only to the extent that it is demonstrable empirically (pratyaksh). Universality is just a European prejudice as they are ill informed about other cultures, so they declare universality from a parochial point of view.
SK: The crude way in which universality is put forward is by saying that 2+2=4, no matter where you are in Greece or Arabia, India or China…
Raju: It is not true, and I have argued it at great length in my paper presented in Hawaii. Let us say we are using a computer to add. 2+2 is a complicated case, so let us take 1+1, The answer could be 1 or even 0 depending on what kind of logic gate one is using. So, I have to specify and say I am using integers. But what are integers? If I do arithmetic with integers on computers say using a C program on a 16 bit machine it will not give 2 as the answer but something else unless I do rounding off. In order to specify what are integers I need infinite time and infinite memory. In a commercial transaction we get into an agreement saying Rs 2 plus Rs 2 would be Rs 4. But that is an agreement. It is not a universal truth. If I have two stones and if I take up two more stones then I get four stones but if I break one of them into two then I get five stone pieces. So I have to be careful about them as universal truths. At a practical level there is no problem. Even if there is no formal agreement or legal frame work, I would simply say you broke the stone. An agreement is not a universal truth or ultimate truth etc.
SK: The statement that numbers are metaphysical transcendental, entities is itself a metaphysical statement.
Raju: That is exactly the point. So long as you are in the domain of convenience it is fine. If you look at Indian texts they will have numbers with 18 digits. What will you do if you need more? you go to 20, 30 or 40 places for a particular purpose. Normally you don’t need more than 18 places. Yajurved goes only till 12 places. Aryabhat goes to 18 places. It is a matter of convenience, but you never go to an infinity of places. That is also how computer arithmetic is done. You round off after some time, and that is perfectly fine but then don’t talk about universal truth.
There is an example given in ethno-mathematics. Suppose I have borrowed two fish from you and I have returned two fish. It won’t do if I have borrowed two big fish and then returned two tiny fish. There is a sense of exchange and fairness involved, not universal truth.
SK: What is the European view on standard of proof etc.
Raju: There is the Platonic deprecation of the empirical. Then there is the clerical elevation of metaphysics over the empirical. The clergy said the metaphysical is a higher truth than the empirical truth. That is fallacious. Metaphysics is decided by a coterie.
What Hilbert did is that he analysed the Elements from this perspective: for example, the proposition 1.4 [of the Elements] or the SAS [Side-Angle-Side] theorem involves physical movement in space, like the Yuktibhasha proof of the “Pythagorean Theorem”. They said the empirical has got into mathematics, which [empirical] is perishable, not eternal, it involves motion hence physics, whereas geometry should be concerned only with properties of immovable space and so on.
So Hilbert said if this theorem is made a postulate then everything becomes metaphysical. Thus he removed the last vestiges of empirical elements in the ‘Elements’. Or at least he thought he did. But actually he could not because he had this notion of congruence which fails after proposition 1.35, the one which is used to derive the area of a triangle. There [in 1.35] congruence is not in the sense of being of the same shape but same area. Earlier propositions are about congruent triangles where you [may] just transfer attention from one shape to the other without moving them. Now [in 1.35] they are incongruent but they are equal in area. The word used in Elements is not “congruent” but “equal”. Equal again is related to equality of the soul as in say Advaita Vedanta which is also a political statement of equality of all people who might look dissimilar. The esoteric meaning is equality of dissimilar things. The way out taken by Hilbert is to define area. But how do you define area without defining length? But if you do define length then the entire Elements becomes trivial as Birkhoff showed with the metric. Thus by throwing out the empirical you start introducing peculiar and artificial things [like defining area without allowing length to be defined] Thus, Hilbert made mathematics completely metaphysical through his ‘axiomatic’ approach.
Now a lot of proofs in mathematics are based on reductio ad absurdum, which depends on two valued logic which would not be acceptable in the Indian tradition at all. So how are these proofs universal?
It is all based on and tightly tied to the [historical] perception that Aristotle the Greek did some logic etc. Of course, one does not even consider that what is called “Aristotelian logic” [might] actually have come from Naiyaikas, through the Arabs. It is a misnomer to call it “Aristotelian”. In my article on Logic for the Springer Encyclopedia of Non-Western Science, Technology, and Medicine, I have made this point that the Aristotelian syllogism is [historically] not to be found anywhere [in Greece]! There is a Stoic syllogism [in Alexandria], but then these things [Aristotelian syllogism] suddenly appear in Toledo and that is problematic.
SK: But syllogism is a very prominent part of Nyaya..
Raju: Yes that is the point, and we also know that Nyaya went to Baghdad. Anyway, the standard approach in mathematics is not universal but has been universalized. First there was the ignorance of Europeans and this ignorance has been universalized through the process of colonization. On the one side [in Americas] people are just killed off, and on the other side they are given Western education where they were given a fabricated history which made them feel inferior. The Indian elite in the 19th century swallowed this and found the solution in aping the west. This has persisted even after independence. My demand is Swaraj in science and in science education.
SK: The creative process is not deductive, otherwise rule-based machines could have done it. But post-facto deduction may be used to teach. However if again our students at the frontiers of research are not going to use the deductive approach then what is the use of even teaching this method?
Raju: Why is mathematics difficult? My answer to that is that math per se is not difficult. But if you look at the text of NCERT for 12th standard, and particularly in Hindi, you find terms like continuity, differentiability, formal real numbers, set theory etc. All this is extremely difficult to follow [in Hindi] even though I have studied all that. It is so terribly convoluted. Where are their primary axioms? They are in set theory, which enables me to axiomatically perform infinite processes, which I cannot ever hope to perform. With the axiom of choice I can have a choice function, I can claim its “existence” etc. It is only through such metaphysical and imaginary infinite processes that one can preserve the perfection of mathematics required by Western theology.
Apart from all these theological principles that have come in, you cannot teach set theory for 10th standard students, so you cannot teach the axiomatic deductive process today. I can do that only at the MSc level and very few people come to that level. The vast majority hence cannot be taught mathematics. You have to tell them a set is a collection of objects! A student has to be taught what is a ring and a field. What utter nonsense! It is very bad pedagogy.
SK: I see a great danger in this. The common perception is that Indians are good in mathematics and good with numbers. That comes from a different tradition than this abstract set theoretic one. By adopting this in our schools we are subverting ourselves!
Raju: That is right and that is the point I have made to the Knowledge Commission. Our culture has some good points and by dropping them we are subverting ourselves.
SK: A very senior executive the chairman of a large bank in Japan told me “We Japanese cannot do software because it is abstract we can do manufacturing very well. We can make things cheaper, faster, smaller etc but not deal with abstractions. Whereas Indian can do it well because they have a philosophic tradition which we lack.” I ventured to say “but you have Zen” and he just brushed it aside.
Raju: That is interesting. I hope it is true. But we are actually adopting counter cultural traditions. There is no discussion of all these things in the public space. I would like to build a quantum computer based on Buddhist logic of chatuskoti, but where is the space to discuss this?
We need to discuss what we need to teach. Somebody just sits behind closed doors and decides what should be taught and that is not correct. There is no reason. Just that we should continue to ape the west. This is how things are made ‘universal’ by a class which is educated in the western tradition and are treated as experts. If experts cannot engage in critical thinking then how do you expect the students to do it?
It is not possible to do computer arithmetic without discarding some part of a number. As soon as we start looking at what a floating point number is, we find that it is not part of a ring or a field or anything! The basic so called associative law is not obeyed. By the way, whose law? why “law”? These are all theological concepts, that the numbers must obey the law etc. All the standard algebraic structures are useless [for computer arithmetic].
In reality, there is a practical way of doing things which is embodied in the way these data types like floating point numbers are used, which is different from theoretical computer science. This encompasses a different philosophy which is closer to what I am talking about. I am talking about practical computation, where we can discard these things. But on what logic? not based on perfection or universalism! You tell me how many decimal places you need and I can procure them. That is where shoonyavad or zeroism comes in. Based on this zeroism I am conducting a course on “Calculus without Limits” in Central University of Tibetan Studies in Sarnath. I am demonstrating it to show how much simpler life can be without universalism or set theory etc.
If we say we are a secular state why should we bring in theology in mathematics, after all if I use Buddhist logic many of the theorems in mathematics will fail! We should teach secular and practical mathematics. We are doing it because the universities in the west are doing it. But those universities were erected for theological purposes. According to [Isaac] Barrow, Cambridge University was established to breed clerics!
SK: I think seeing the pragmatism embedded in western societies today I think if you build a quantum computer using Buddhist logic that can threaten the encryption involved US financial system then you would have proved your point and billions of dollars will be spent on research on alternative logic.
Raju: That is accepted. We do need to find applications, but for me the very fact that people will be able to understand much of mathematics using this new system itself would be a worth it. I don’t care if the west wants to do it or not. My son should be able to do calculations easily which he could not do earlier.
SK: I will give an example to illustrate what I was saying. Fuzzy Logic was invented by Lotfi Zadeh, a Iranian professor at University of Berkeley. There were people who called it cocaine of mathematics implying that he was high on drugs and invented this since it did not follow the normal Aristotelian binary logic. The Japanese picked it up and used it in all appliances like washing machines, TV etc. The Americans picked it up only in the 80s because they had launched an armed commando raid on Tehran in 78-79 during the hostage crisis. But the control systems of their military helicopters carrying the commandos could not stand the heat and dust of the desert. They crashed and the mission was a failure. Then they realized they needed fuzzy logic based adaptive control systems and they brought them in. In that sense they are not theological.
Raju: My concern is not to convert the west. My concern is if these theological concepts have crept into mathematics then that mathematics should NOT be taught in this country. We should teach secular mathematics. After all it is being used to condition people, inculcate inferiority in them through fake history etc.
SK: It is definitely driving people away from mathematics.
Raju: And these kids keep looking at pictures of a fake Euclid and a fake Pythagoras as white Caucasians which we see in text books, and grow up in awe of the west and say the solution to any problem is to ape the west. If we can break out of those things that itself would be an achievement.
SK: One last comment. Many have objections to the way the Indian mathematical results are written in the form of a sutra without explaining how they arrived at it or what is the justification for it. Is there any insight into how they achieved these results? Secondly, one person who wrote many results filling up many note books without giving proof is Srinivasan Ramanujan though it was in the field of analysis in the western tradition.
Raju: I am not arguing for an absence of process. To deny the value of deductive proof is one thing, and to say that there should be complete absence of process is another thing. I would assert that though there was the sutra tradition there were also Yuktibhasa, Yukti Deepika etc where they explain the process, perhaps due to Jesuit pressure! They were written after the arrival of Europeans in Cochin. A sutra has to be terse to make it easy to remember. It is a cultural matter [in the oral tradition] that here we are dealing with minds of human beings and hence the communication should be from one mind to another and not filtered through a derivation on a dead parchment where it is liable to be misunderstood. Right or wrong that seemed to have been the cultural tradition and an oral tradition. After all even Vedas are not written down. That is not a critical issue dealing with validity but a pedagogical matter.
Certainly a process has to be there and a justification [praman] has to be there. In my book [Cultural Foundations of Mathematics] I have shown [in Chapter 3] that there is complete praman for the infinite series in India, but the derivation is on different philosophical principles. I don’t say that first I should have set theory which allows me to do some infinite processes and then I should have an infinite set of numbers and then prove convergence and so on. That is the rigmarole of Western mathematics.
I want to sum the series and the stated criterion is that the sum should remain constant when I add two consecutive terms. How does it remain constant? Up to the level of accuracy and the decimal (or sexagesimal) places I need. This is similar to epsilon-delta [and the “Cauchy” criterion] but deals with a finite number of terms [and does not involve a infinite metaphysical process]. That is a perfectly good criterion.
SK: That is what physicists do when they sum any series like Raleigh-Schroedinger perturbation series. You calculate to the second order of approximation and if there is serious problem you go to the next order.
Raju: That is how all computer algorithms are done. It only ceases to be valid if you demand perfection! That is a perfectly practical attitude. It is not that process and proof are missing. It is just proof from a different philosophical position.
The first text book on philosophy that I picked up from my father said, there is no philosophical tradition in India but only poetry! For philosophy you have to read the Greeks! So now I can say that there is no mathematical tradition in Europe and it is all theology which was imported here through colonialism!
What happened with Elements is that it had come to India through Islam but it was not translated into Sanskrit till very late at the time of Sawai Jai Singh in 1723, long after the arrival of Jesuits in Jehangir’s court. There were two parallel distinct traditions. Akbar’s courtier (Abul Fazl) who wrote the Ain-e-Akbari talks about learning from the Elements. It was there in Arabic and Persian traditions but was not considered valuable by Indian mathematicians. It was considered something religious. Also, practically Pythagoras theorem comes at the end of the Elements where as Yuktibhasa starts with it, with a different way of proving it without the forty odd earlier results.
So I would say it is a religious belief which is being universalized and I find it highly objectionable. I would say, in fact, our principles are universal since they are empirical and physical. I would characterize present-day mathematics as European ethno-mathematics tainted by theology.




























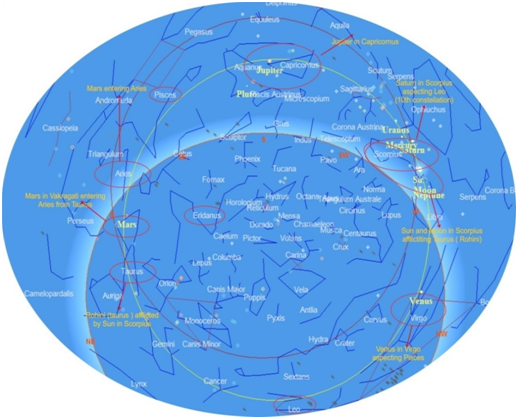




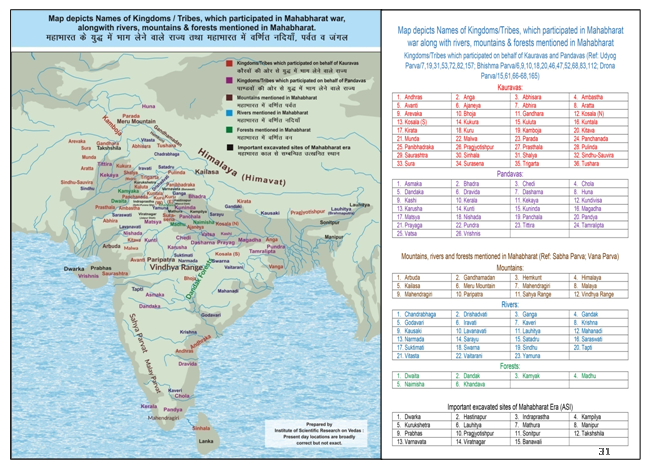
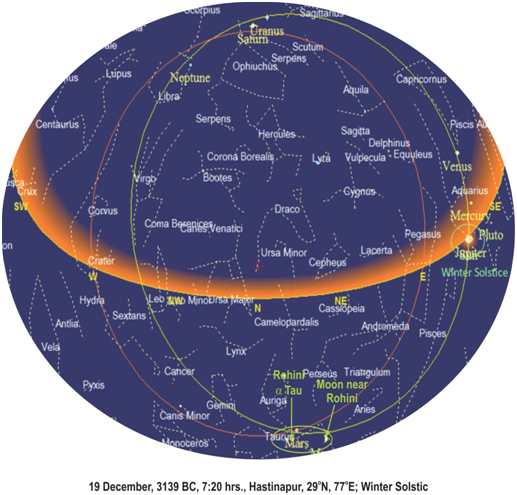




































 RSS Resolution ABPS-2017
RSS Resolution ABPS-2017
















Reply
Reply
Reply